(Reprinted from Yoon and Sharp 1990)
DESIGN AND OPERATION
School of Industrial and Systems Engineering
Copyright: 1991 Georgia Tech Research Corporation,
Atlanta, Georgia 30332
Georgia Institute of Technology
This report is concerned with order picking in a
warehousing system. Although an order pick system (OPS) contains
a few basic functions, the wide spectrum of external and internal
factors in order picking makes the real OPS very complicated.
For analysis purposes, order picking is defined as the selective
retrieval of the appropriate amounts of products from a pick (or
storage) area to fill specific customer orders. Orders are usually
represented by a list of stock keeping units (SKUs) or line items.
The list specifies the type and retrieval quantity of each line
item, along with other information such as the due date, the customer
name and address, etc.
Order picking and material handling, in general,
have received considerable attention since the 1970s. Kearney
(1986) estimated that the overall logistics cost in the United
States is 21% of the Gross National Product, and that 28% of this
logistics cost is accounted for by storage and retrieval (S/R)
systems. The Warehouse Education and Research Council (1986)
identified order picking as the number one area for improvement
in warehousing.
Recent trends in distribution and manufacturing will
make order picking even more important. In distribution systems
there is increasing emphasis on better delivery time and accuracy
standards. In manufacturing the move to smaller lot sizes, point-of-use
delivery, and cycle time reductions, make efficient order picking
crucial to being competitive (Shirk 1989). Other economic factors
such as marketing pressures for more diversified product lines
and shorter product life cycles result in additional importance
and complexity of order picking (Weber 1989). Hence, the efficiency
and cost of order picking are crucial issues to a corporation
in today's intensely competitive marketing arena.
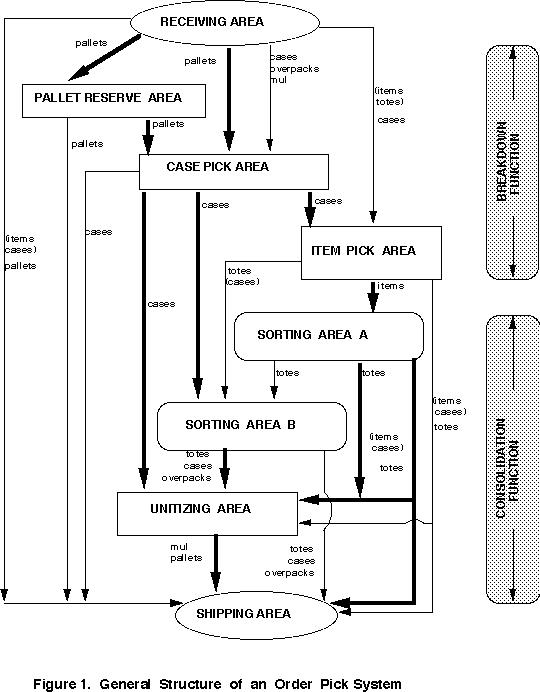
Considering the flows of items and orders in OPS,
a general structure of OPS is proposed in Figure 1 (Yoon and Sharp
1990). The general structure of OPS consists of 8 departments
(or functional areas): receiving area, pallet reserve area, case
pick area, item pick area, sorting area A, sorting area B, unitizing
area, and shipping area. The eight departments can be functionally
categorized as breakdown area or consolidation area. All possible
and most likely (thick arrows) flows are represented by the appropriate
types of handling unit in Figure 1.

To appreciate the functions of each department, let
us consider the flow of a hypothetical high-activity product.
The product is received in pallets and stored in a pallet reserve
area (e.g. the upper levels of pallet rack). It is then moved
to a case pick area (e.g. lower levels of pallet rack). Individual
cases are removed from the case pick area and placed in the item
pick area (e.g. gravity flow rack holding cases). The pickers
selectively retrieve items from the flow racks and place them
on conveyors which carry the items to sorting area A. There the
items of each order are contained in totes; they might then go
to a unitizing area to be palletized or combined into a mixed
unit load (mul), and then to shipping, or directly to shipping.
Some customers might order this high-activity product
in case lots. These might be retrieved directly from the case
pick area and sent to sorting area B, for sorting cases and totes.
The equipment in sorting area B might be different from that
in area A, which is for sorting smaller items. It is conceivable
that the same equipment could be used for both purposes, either
simultaneously or at a different times.
Figure 1 should not suggest that every OPS should
have this structure and all the diverse flows. Instead, it shows
the many possible ways that products can flow through an OPS.
The question of which SKUs for which orders should flow in which
ways is in realm of specifying the operational strategy. We designate
this as the specification of order pick system structure.
Figure 1 also shows three types of order picking:
pallet retrieval, case picking, and item picking. By focusing
primarily on order profiles, OPS can be classified in four categories
for analysis purposes, as shown below (Sharp, Choe, and Yoon 1990).
The factors of order size (line items per order), order volume
(orders per time period), and extent of advance information, results
in 23 = 8 combinations when 2 levels of each factors are considered.
Precise definitions of the descriptors are not possible.
It is suggested that the number of orders be compared to the
number of packing/shipping lanes. If during a process cycle a
packing/shipping lane can be dedicated to an order, we say there
are few (F) orders. If a packing/shipping lane is to be shared
by several orders during a process cycle, we say there are many
orders. A high volume of orders results in additional complexity
of the OPS, especially of sorting areas.
Order size can be determined by cubic volume and/or
number of line items. It is suggested that a small (S) order
be defined as one that contains 10 or fewer line items; a line
item is a SKU requested by an order. If the quantity per line
item results in a cubic volume less than 0.01 cu. m.(0.35 cu.
ft.), then a small order is also limited roughly to 0.1 cu. m.
(3.5 cu. ft.). A large (L) order, containing more than 10 line
items, would often have a volume greater than 0.1 cu. m. In some
situations a large order might fill a truck. These definitions
allow for some awkward, in-between situations. We believe that
the demarcation based on the number of SKUs is more important
since it relates more to operating strategies than a demarcation
based on cubic volume.
The difference between advance (A) information and
statistical (S) information relates to the ability to process
the order data for more efficient operation. In the MSS example
of a stock room serving a manufacturing facility, the requirement
for fast response (e.g. 20 minutes) probably would preclude the
types of batching strategies used by a catalog retailer, who usually
has several hours at night for data processing and a late-afternoon
shipping deadline. If there is adequate time for preprocessing,
we say there is advance information. Otherwise, the information
is statistical.
The information availability is directly related
to the control rules in the operation of the OPS, since decision
making based on statistical information is often quite different
from one based on advance or deterministic information. For the
MSS-OPS, the primary objective of analysis is to estimate the
response time by finding the stochastic behavior of the system
under given statistical information. Advance information or the
availability of a 'long' response time allows many opportunities
for operating a system in an 'intelligent' way; for example, batching,
sequencing, workload balancing, etc. Consequently, the major
challenge in the OPS with advance information such as MSA-, MLA-,
and FLA-OPS is how to take advantage of the advance information.
Our classification considers only 4 out of possible
8 combinations. The scenarios of a few small orders, with statistical
or advance information (FSS and FSA), do not provide much incentive
for analysis and are excluded. The situation of a few large orders
with statistical information (FLS) is relatively unusual. The
situation of many large orders with statistical information (MLS),
it can be argued, can be approached with many of the same strategies
as MLA-OPS. Thus, the four categories listed suffice for analysis
purposes.
This report presents an outline of order picking
from an analytic viewpoint. By examining thoroughly the complicated
nature of OPS, the primary objective is to lay a sound base which
reveals the unique features of order picking and so to systematize
research efforts in the future. Previous attempts can be found
in Gudehus (1973), Frazelle (1988), Goetschalckx and Ashayeri
(1988), Muller (1989), and Yoon and Sharp (1990). Most of these
efforts focus on some specific aspects of order picking rather
than a framework. Reviews of the literature on general material
handling can be found in Matson and White (1982), Ashayeri and
Gelders (1985), Francis, McGinnis and White (1985), and Kusiak
(1985).
For the development of a general framework of OPS,
Yoon and Sharp identify seven types of factors in the design of
OPS:
1. Material properties of items stored.
2. Transaction data for SKUs and orders.
3. Operational strategies for storage assignment and retrieval.
4. Specification of hardware for subsystems and design of operator work areas.
5. System requirements with respect to throughput, inventory capacity, accuracy, and system response time.
6. Constraints based on building layout and operator safety.
7. Budget constraints related to investment and
total annual cost.
Instead of an itemized discussion of the issues above,
we classify them into 3 categories: strategic factors, design
issues, and operational issues. They, along with other issues,
will be presented with an emphasis on their inter-relationships.
Such discussion will be helpful in comprehending the OPS as a
multifaceted system of great dimensional complexity.
The next section identifies the strategic factors
of OPS and presents an OPS design procedure. Included is a discussion
of the various issues involved in order picking. The third and
fourth sections, along with a literature review, go into more
details on the issues in the design and operation of OPS, respectively.
Issues in design include the specification of OPS structure,
equipment selection, determination of the space requirements,
and layout. Issues in operation include storage rules, pick strategies,
A/S strategies, packing/palletizing, human factors, and hardware
solutions. The issues and results applicable to individual equipment
type are discussed in the fifth section. Finally, the sixth section
describes future research opportunities that seem to offer promise
for significant efficiency gains. Some of the results here are
presented in Sharp, Choe, and Yoon (1990).
A design of a system shows what we know about the
system; a design procedure for a system shows what we should know
about the system. Therefore, a design procedure for OPS is crucial
to the identification of the issues involved in the design and
operation of OPS, and also to their inter-relationships and hierarchy.
We first explain the strategic factors, usually beyond of the
control of the system planner, which delineate the requirements
and objectives of OPS. Then, we present how to design an 'efficient'
OPS to meet such requirements.
The strategic factors of OPS can be classified into
three categories: system profiles, order profiles, and item profiles.
The system profiles determine the status of an OPS
within the whole system and its interactions with other subsystems.
In a broad sense the system profiles include the strategic planning
factors of the corporate organization; in a narrow sense the system
profiles include the type and number of suppliers, the type and
number of customers and their service levels, etc. (Goetschalckx
and Ashayeri 1988).
The supplier type can be an in-house manufacturing
facility, external (domestic or overseas) manufacturing facility,
or external distribution center. The major effects of suppliers
are on the inventory policy and the replenishment patterns of
inventories in the OPS. For example, if the supplier is an in-house
manufacturing facility, the control on replenishment of the OPS
might be limited by other considerations such as the efficiency
of the manufacturing process. Overseas suppliers, on the other
hand, usually mean long lead times and large order quantities.
The inventory policy depends on the customers as
well. The customers can be wholesalers, retailers, a combination
of both, or a manufacturing facility. The types and number of
customers are important, since they basically determine order
profiles and service levels. For example, the design and operation
of a local distribution center are usually different from those
of a national depot.
The order profiles include the volume of orders,
the number of line items per order, the retrieval quantity of
a line item per order, due dates, priority classes, and any similarities
among orders. In general, the order profiles strongly influence
the system design. For example, an order of a truck-load of goods,
a typical one for a national distribution center, is not processed
by the same type of equipment and procedure as one of a cart-load,
a typical one for a local distribution center for small retailers.
Another important factor of order profiles is the information
availability or the response time constraint. Generally, the
more time that is available before an order must be shipped, the
greater the opportunity to improve efficiency by 'intelligent'
control rules. Hence the design and operation of an OPS should
be compatible with the information availability.
The item profiles include the number, size, weight,
stackability, suitability for nesting, and environmental requirements
of the SKUs. These factors must be considered in selecting equipment
for S/R and handling among other issues. For example, high-security
items should be stored in a closed equipment such as storage drawers,
vertical carousels, or miniload AS/RS, and not in an open equipment,
such as shelving. Fragile items might be damaged by a high-speed
sortation system. Diversity in size and weight of items can also
lead to more dimensionality and problems in using high-speed sortation.
The item profiles thus restrict the compatible equipment types
and their layout, and influence the total cost of the OPS.
Considerable previous work has been done on systematic
and/or analytic methods for the design of 'conventional' warehouses
of which a major function is pallet retrieval: e.g. Kay (1968),
Gudehus (1973), Amagai (1985), Branigan (1988), Juenemann and
Meister (1988), Perlmann and Bailey (1988), Park and Webster (1989a),
Schulze and Westfal (1989). Some of them develop computer aided
systems for the design of conventional warehouses.
The design of an OPS is a more difficult task than
that of a conventional warehouse due to the greater complexity
of order picking. Elliott (1986), Goetschalckx and Ashayeri (1988),
Hanelt and Kryder (1989) are concerned with the design procedure
especially for OPS. Elliott, and Hanelt and Kryder explain the
details of OPS design by following each step of the classical
engineering design process. Goetschalckx and Ashayeri present
a structured approach called SYDOPS, along with a general framework
of an OPS. A practical and comprehensive guide can be found in
Zollinger (1982), the Naval Supply Systems Command (1985), and
Carew (1989). None of these efforts, however, explicitly specifies
the structure of an OPS, and none considers the flows of orders
and items in the system. A number of case studies for the design
of warehouses and OPS are reported in the literature, such as
the Proceedings of the International Conference on Automation
in Warehousing.
A design procedure by Yoon and Sharp (1990), with
an emphasis on the interwoven structure of the OPS, consists of
three main stages: input stage, selection stage, and evaluation
stage. Their procedure is illustrated in Figure 2. First, the
input stage includes the determination of strategic factors and
the specification of the structure of the OPS. A data analysis
phase leads to specifying the objectives, requirements, and structure
of the OPS. The major outputs of this stage include a functional
specification of subsystems and the flows of the items and orders
in the system.
They then proceed to the selection stage, which consists of
These four design tasks must be performed together
for each alternative. For example, a five aisle person-aboard
S/RS with batch picking in five zones, one per aisle, will have
a different information transformation of the order data into
pick lists than a 20-aisle shelving system with single-order-pick
strategy. Similarly, physical transformation of items depend
on the equipment, the operational strategy, and the results from
the input stage. The outputs of the selection stage are an explicit
specification of each potential subsystem including equipment
types, operational strategies, performance evaluation, cost and
space requirements, etc.
The evaluation stage is concerned with the overall
evaluation of subsystems from the system point of view. It consists
of the following four steps:
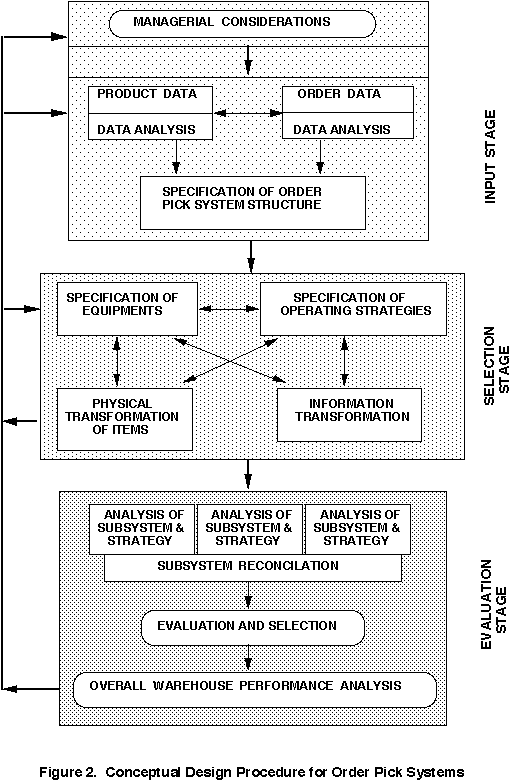
The first important task in the evaluation stage
is subsystem reconciliation. An example is the use of a pallet
rack for both the reserve storage (RS) and the pick system (PS);
there must be proper balance between spaces required and time
needed for each function. Another example is when single-order
picking and batch picking are performed using the same equipment.
A third example is the capacity matching of the sorting system
with the output of the pick system. Some type of multi-criteria
evaluation procedure is usually employed in the evaluation stage
(Pliskin and Dori 1982). It is not unusual for the design procedure
to be partially repeated. The actual implementation of the design
selected requires again a considerable amount of planning and
effort; this issue is beyond the scope of this research.
The design procedure for OPS reveals the issues crucial
to the 'successful' design of OPS: determination of system requirements,
specification of order picking system structure, selection of
equipment for each subsystem, operating strategies, and determination
of the physical dimensions and layout. The determination of system
requirements, the upper-most level of the decision hierarchy,
should be based on a comprehensive analysis of both the current
status and the long-term perspective of management. Especially,
the requirements should reflect possible changes of the strategic
factors in the decision horizon, and also of order picking technology.
See White (1988) and Hatanaka (1989) for current trends in material
handling and order picking.
The specification of subsystems and equipment types
usually consists of several steps as follows:
The analysis of order profiles, along with other
system requirements, will reveal how many orders require pallet
retrieval, case picking, and item picking, respectively, and also
what quantities of which items should be provided for each type
of order picking. Suzuki (1988) presents a structured method
based on the so-called order pattern graph which enables a planner
to identify easily the relationships among orders, SKUs, and retrieval
quantities.
Based on these results we then can determine whether
each type of order picking is performed by a separate system or
by sharing a system with others. It is difficult to obtain the
structure of the OPS by quick analysis, and few guidelines are
available in the literature (Yoon and Sharp 1990). More structured
methods such as group technology may be applied to the classification
problem (Mutel and Anciaux 1989).
The next step after specifying the structure of the
OPS is to select the 'best' equipment type for each subsystem.
The decision is usually associated with multiple criteria, some
of which might be conflicting. The equipment selection is closely
related to the total space and budget constraints and also to
the layout planning of the OPS. For example, when there is a
limit to the available space, the selection problem of a subsystem
should be based not only on its own factors but on their effects
on the total space requirements and layout. These decision problems
lead indeed to a fertile, open research area.
To facilitate our discussion, material handling equipment
available for OPS is classified into four categories: S/R equipment,
accumulation/sortation (A/S) equipment, handling equipment, and
auxiliary equipment. This study focuses on the S/R and A/S types
of equipment, which comprise the main hardware of an OPS. The
handling equipment links the subsystems of the OPS. The auxiliary
equipment items are a vital part of any material handling system,
but they do not physically handle items.
S/R equipment is classified into three types:
The major difference between picker-to-part systems
and part-to-picker systems is whether the picker has to travel
to the pick location or vice versa. White (1979), and Frazelle
and Sharp (1990) give brief discussions on the pros and cons of
picker-to-part and part-to-picker systems. Krajacic (1988) gives
a general description of the automatic item picker.
The equipment types for A/S operation include
A/S operation is not clearly separable from S/R operation,
since partial and complete sorting can sometimes be done during
the order pick process.
The primary function of handling equipment is to
link subsystems by moving items from one to another. The major
types of handling equipment are
The auxiliary equipment to support the other equipment
types includes
It is a complicated issue to determine the 'best'
equipment even under well-defined requirements and specification
of material handling activities. The complexity is ascribed to
the great variety of factors such as the number of equipment alternatives,
the multiple criteria for selection, and the inter-relationships
with other subsystems. From an analytical view point, the equipment
selection problem consists of three sub-issues: unit load size,
equipment type, and physical dimensions.
Determining the container or the unit load size is
one of the strategic issues in material handling as well as order
picking. The unit load is defined as the number of items or the
amount of bulk material contained in the basic handling unit of
a set of material handling activities. According to Tanchoco
and Agee (1981), the potential advantages of the unit load include
more effective utilization of storage space, and reductions in
handling, packaging, and transportation costs; its potential disadvantages
include loss of the flexibility in the handling system, and labor
costs and additional equipment for unitizing/de-unitizing.
The scope of previous works related to the unit load
problem is very limited. Most of the results focus on certain
aspects of the problem in handling pallets: Steudel (1983) for
general material handling systems; Tanchoco, Davis and Wysk (1980),
Grasso and Tanchoco (1983), Tanchoco et al. (1983), Emamizadeh
and Knott (1986) in conjunction with inventory policies; Roll,
Rosenblatt and Kadosh (1989) for a unit-load AS/RS.
Various attempts have been made for the selection
of equipment type; a review on earlier works can be found in Matson
and White (1982). Recently, Malmborg, Hubbard and Agee (1985)
develop a computer aided procedure based on simulation and multi-attribute
decision models. Houmas (1986) presents the cost and performance
comparisons of various equipment types for item picking such as
storage drawers, gravity flow racks, carousels, and miniload AS/RS.
Assuming a warehousing system with just two different types of
S/R equipment, Azadivar (1987) and (1989) develops analytical
models to allocate the space to each S/R equipment type. Azadivar
formulates the allocation problem as stochastic programs of which
the parameters are estimated by simulation.
The limited scope of analytical models results in
the development of rules-of-thumb for equipment selection. One
of the criteria frequently used for such rules-of-thumb is the
level of automation. Using the level of automation as the major
criterion of equipment selection, Cox (1986) develops a framework,
called a hierarchy of productivity ratios, to determine the suitable
level of automation. Gelders and Ashayeri (1989), among others,
give typical equipment types at three different levels of automation
for each combination of two factors: item size and throughput
requirements.
As Malmborg, Simmons and Agee (1986) suggest, the
expert system approach can be applied also to equipment selection:
Fisher, Farber and Kay (1988), and Matson, Swaminathan and Mellichamp
(1990) for the selection of handling equipment including manual,
trucks, conveyors, AGVs, and cranes; Malmborg et al. (1989) for
the selection of industrial truck types. However, no expert systems
for S/R equipment selection are reported in the literature.
We discuss here two major issues associated with
the specification of the physical dimensions and layout of OPS:
the determination of the total space requirement and an efficient
layout.
The estimation of the total space requirement is
a prime example of the degree of complexity peculiar to OPS design.
The total space requirement is influenced by virtually all the
issues associated with order picking. For example, a long-term
perspective of business influences the physical size of buildings
and other structures to meet foreseeable future demands; order
profiles, item profiles, the inventory policy, and the replenishment
pattern influence the OPS size; the equipment types used in the
OPS influence the OPS size; operational strategies, such as the
storage rule, influence the equipment size, and so the total space
requirement; the layout influences the OPS size. The discussion
above implies two conflicting restrictions: the space requirement
cannot be precisely estimated until most details of the OPS are
specified; however, the space requirement is crucial to the specification
of those details.
The estimation of the space requirement consists
of two major steps: estimation of peak and average (aggregate)
inventory levels of items stored, and transformation from the
inventory volume to the space requirement. Yang (1988) and Hall
(1989) contain a literature review of the inventory packing problem,
which consists of estimating the maximum level of the aggregate
inventory in the system and then minimizing the peak level. Even
if we can estimate the inventory volume, it is difficult to transform
the inventory volume into the space requirement, especially for
case and item picking. Most of results obtained so far are concerned
with the space requirement for pallet retrieval only: Mullens
(1981), Rosenblatt and Roll (1988), Park and Webster (1989a),
Camp (1990). All the works are based on simulation.
Our discussion based on two separate steps should
not imply that they are truly separable. For a conventional warehouse,
Wilson (1977) demonstrates that the inventory policy and the storage
rule should be determined simultaneously to minimize the total
costs. The analogous problem in the unit-load AS/RS is exploited
by Hodgson and Lowe (1982). Vemuganti (1987) presents an optimization
model for determining the production lot size that includes all
of the production, inventory, and storage space costs; however,
the model does not consider handling costs. For a block stacking
system, Schall and Chandra (1989) are concerned with a generalized
model including the inventory packing problem, unit load size,
and storage space. In fact, their model is a generalization of
Tanchoco et al. (1983) by using Page and Paul (1976) on the inventory
packing problem.
Planning the layout of a system certainly deserves
the great attention shown in the literature (Tompkins and White
1984). With the emphasis on order picking, the layout problem
of OPS has two subproblems: the layout of the system containing
the OPS and the layout within the OPS. For example, the first
subproblem, usually called the facility layout, is crucial to
an OPS supporting a manufacturing system such as MSS-OPS; the
second one to an 'independent' distribution center such as FLA-OPS.
Most results in the literature are concerned with
the layout of conventional warehouses. Since the equipment in
a conventional warehouse is either block stacking or pallet racks,
most effort for the layout focuses on the aisle configuration,
e.g. Bassan, Roll and Rosenblatt (1980). In addition, a block
stacking system needs to specify the number of lanes, and the
depth of each lane; see Ashayeri and Gelders (1985) and Goetschalckx
and Ratliff (1987) for details.
One of crucial issues related to OPS layout is the
pick versus reserve problem (P-R) problem or what the inventory
policies and replenishment patterns of RS and PS are. A review
can be found in Bozer (1985). The primary objective of the P-R
problem is to minimize the storage, replenishment, and handling
costs of both systems. It is a formidable task to find a universal
solution to the P-R problem. The results obtained so far point
out that solutions are far from trivial, and that the decision
has significant effects on the system performance (White and Kinney
1982). Kooy (1984) and (1985) give practical methods and guidelines
for real P-R problems.
As explained in the previous sections, the decisions
in the design stage should reflect the effects of operational
strategies. This section presents more details on operational
issues.
The storage rule is defined as a rule for assigning
each SKU to storage locations, and the storage location assignment
problem (SLAP) is a problem to find a storage rule which optimizes
the objective function(s) given a detailed specification of SKUs
and equipment. The primary objective of the SLAP is to minimize
the average process time per S/R activity (or order). Even if
the total cost of order picking may be the ultimate concern, a
significant portion of the total cost is usually proportional
to S/R time. Rules-of-thumb for SLAP can be roughly stated as
follows:
Rule RT1 results from the ABC (or Pareto's) law which
characterizes the typical distribution of S/R activity of SKUs
in real OPS. Loosely translated, it states that some small percentage,
say 20%, of the SKUs in the system usually represent a majority,
say 80%, of S/R activity. Consequently, most design efforts should
focus on the high-activity SKUs, which deserve the 'prime' locations
near the I/O point.
The second rule, RT2, can be achieved by minimizing
empty storage space. It can be achieved either by using a 'balanced'
inventory policy, or by sharing a location with as many SKUs as
possible. The S/R area is 'perfectly balanced' if the number
of arriving units is equal to the number of departing units during
any time period (Goetschalckx 1983). In the perfectly balanced,
but unrealistic, system there is never an empty location at the
end of each period. For OPS not perfectly balanced, however,
RT2 leads to frequent conflicts with rule RT1. For example, contrary
to RT1, RT2 may fill a location near the I/O point with a slow
mover if the item is the only one to be stored at the time. Effort
for solving this conflict leads to various strategies for the
SLAP.
The storage rules widely used in industry can be
classified into three major categories: floating slot storage,
fixed slot storage, and hybrid storage of both. Floating slot
storage basically follows RT2; fixed slot storage follows RT1;
hybrid storage comprises both.
With floating slot storage many different storage
locations can be assigned to a SKU over its many replenishments.
A typical rule of floating slot storage is random (or randomized)
storage (RANDS). RANDS, strictly following RT2, assigns an incoming
item to the location closest to the I/O point among available
ones, regardless of the item's storage period (or turnover rate).
RANDS derives its name from the fact that the locations of SKUs,
especially in unit-load AS/RS, 'appear' to be randomly distributed.
It is interesting that the equivalence between the closest-open-location
(COL) rule and the purely-randomized-assignment (PRA) rule is
not fully addressed in the literature. The seemingly conflicting
results imply that
Lim shows also that unfavorable zoning (fast movers
in the back of the rack, and slow movers in the front) can occur
in a model with some restricted conditions. Consequently, the
equivalence between COL and PRA is still in doubt, even though
it is assumed by most works in the literature.
Fixed slot storage (or dedicated storage, DEDIS)
is solely based on rule RT1; each SKU has its own fixed storage
location usually based on the intensity of S/R activity. The
major issue in DEDIS is how to assign each storage location to
which SKU, even though the optimal strategy would follow RT1 in
principle. It turns out that the optimal assignment depends on
various factors, which will be discussed later.
The hybrid of floating slot storage and fixed slot
storage is frequently referred to as class-based storage (CLASS).
First, CLASS partitions all the SKUs into several classes, and
assigns a (usually fixed) area to each class. Then, RANDS is
used within each class area. Partitioning of SKUs into classes
may be based on S/R activity, so that fast moving SKUs are grouped
as the first class stored near the I/O point. In fact, RANDS
is CLASS with the single class, and DEDIS is CLASS with as many
classes as the number of SKUs. Some variations are possible.
For example, Lim considers a variation of CLASS, the so-called
Skip-k policy, with 2 classes. Under the Skip-k policy, an incoming
item of the second class is assigned to the (k+1)st open location.
Lim can not distinguish an advantage of the Skip-k policy over
the fixed-zone policy in the 2-class CLASS.
In general, RANDS results in high space utilization
or low space requirement with the expense of increased travel
time; DEDIS yields the largest savings in travel time, but usually
with substantial under-utilization of space. CLASS is somewhere
between RANDS and DEDIS, depending on parameters such as the number
of zones and the skewness of the S/R activity distribution. The
comparison above is not conclusive, since a number of factors
are involved in the efficiency of each storage rule. Among the
more important are the ABC skew and the operating mode of the
pickers (or S/R machines).
The operating mode can be classified into three categories:
single command (SC), dual command (DC), and multi command (MC).
In SC operation the picker performs only one S/R activity between
successive visits to the I/O point; in DC operation, 2 S/R activities;
in MC operation, more than 2 S/R activities. For example, a conventional
unit-load AS/RS or miniload AS/RS can do either SC or DC operation.
A person-aboard S/RS and a rack system are normally operated
in MC mode. The picker aboard an S/R machine or walking (or riding)
through aisles of racks is usually able to do 5-25 S/R activities
on a trip.
SC operation is typical in a conventional warehouse
mainly for pallet retrieval. Most earlier works on the storage
rule are concerned with the optimal storage rule of a conventional
warehouse under DEDIS and SC operation. The most famous storage
rule in that case is the cube-per-order index (COI) rule, which
is attributed to Heskett (1963). The COI is the ratio of the
space requirement (cube) of a SKU to its turnover rate. The COI
rule ranks the items in an ascending order of the index, and then
assigns them in that order to the locations nearest to the I/O
point. The analytical results supporting the COI rule include
Francis and White (1974), Harmatuck (1976), Kallina and Lynn (1976),
Evans (1984) for SC operation; Malmborg and Bhaskaran (1987) and
(1990) for DC operation; Malmborg and Bhaskaran (1989) for MC
operation. For a real warehousing system, Davies, Gabbard and
Reinholdt (1983) report that the COI rule increases the productivity
of item picking.
The COI rule can be used also for CLASS. The major
issues in CLASS include the number of classes, the shape of each
class area, and the partitioning rule (i.e. a rule to assign each
SKU to a class). Most works related to CLASS use the COI rule
as the criterion for the partitioning rule. Schwarz, Graves and
Hausman (1978), Choe and Sharp (1989), and Kim and Seidman (1990)
show that CLASS yields significant savings in travel time for
both SC and DC operation, and Choe and Sharp (1988) for MC operation.
More specifically, Choe and Sharp develop the analytical estimators
of SC and DC travel times in unit-load AS/RS, and then gives a
set of partitioning rules depending upon the skewness of S/R activity
among SKUs. Their results also imply that CLASS leads to shorter
travel time even under MC operation in person-aboard S/RS, and
that a small number of classes, say 3-5, with a few partitioning
rules, can achieve most of such reductions in travel time, since
the average travel time curve is quite flat near the optimal parameters.
All the results above assume that the total space
requirement is independent of storage rules, which does not hold
in real circumstances. Roll and Rosenblatt (1983), Rosenblatt
and Roll (1984) are concerned with such effects of storage rules
for port warehouses. Using simulation, they compare the space
requirement of RANDS, CLASS, and DEDIS; their definitions are
slightly different from ours due to the unique features of the
port warehouse. Their results imply that CLASS can significantly
reduce the space requirement compared to DEDIS, and that most
of such reductions can be achieved by no more than 6 classes.
Yang (1988) is the first work which explicitly considers
the space requirement depending on the number of classes for unit-load
AS/RS. He develops an algorithm to find an optimal partition
of SKUs for CLASS to minimize the expected travel time of the
S/R machine. In his case study, as the number of classes increases,
the expected travel time follows a U-shaped curve with the minimum
at 6-class CLASS. In other words, the expected travel time decreases
until the increased space requirement resulting from the large
number of classes offsets the savings in travel time.
An interesting concept for the SLAP is SKU vs. unit
assignment. CLASS and DEDIS use SKU assignment. Namely, all
units of a SKU are assigned to the same class in CLASS or a contiguous
area in DEDIS. Contrary to SKU assignment, unit assignment is
based on the expected storage time of each unit, instead of average
storage time of the SKU. Goetschalckx (1983) pursues unit assignment
under the name of shared storage. With floating storage, he gives
several methods for considering the activity level of each unit,
instead of the naive COL assignment. Goetschalckx and Ratliff
(1987) develop the unit assignment rule for a block stacking system.
Another approach for the SLAP is the correlated assignment
(CORAS) (Frazelle and Sharp 1989). The simple principle of CORAS
can be stated as SOTAST, which stands for "SKUs Ordered Together
Are Stored Together." CORAS is devised to take advantages
of the correlated S/R activity which is frequently manifested
in real OPS. Frazelle and Sharp report significant savings in
travel time under CORAS.
Dichtl and Beeskow (1980) present a CORAS model for
an OPS with MC operation. Their model first estimates the pairwise
correlation among SKUs, and then assign SKUs with strong correlation
to locations that are close to each other. Stern (1986) applies
SOTAST to a carousel system. Considering various improvement
strategies for a real warehouse, Oudheusden, Tzen and Ko (1988)
implement CORAS in a person-aboard S/RS. Since the picker aboard
the S/R machine can access two opposite locations at a single
stop, they devise CORAS by considering pairwise correlation, and
then solve the problem as a maximum weighted matching problem.
SOTAST becomes more attractive for a multi stocking
system in which several different SKUs can be assigned to the
same storage location. For example, a tray in a miniload AS/RS
and a storage drawer in a drawer system can house more than one
SKU. Consequently, multi stocking results in great complexity
of the SLAP, which now has to consider the capacity constraint
of each storage location on the size and sometimes on the orientation
of each unit (Herrera-Cuella and Sharp 1983). Note that multi
stocking has some features of the packing/palletizing problem
which is discussed later.
Some equipment types may have more than one I/O point,
which can be used for input only, or for output only, or for both
functions. Even though most results in the literature assume
a single I/O point, the extension to the multiple-I/O system is
not straightforward. Few studies have been done on this issue;
see Francis and White (1974) for a conventional warehouse, Waugh
and Ankener (1977) for a unit-load AS/RS, and Kaylan and Medeiros
(1988) for CLASS in a miniload AS/RS.
Picking line items is one of the most time-consuming
and labor-intensive activities of OPS. Consequently, various
strategies are used to improve the productivity of the pick process.
Among them are batching, zoning, human factors, and hardware
solutions.
Batching and zoning determine which order/item is
retrieved by which picker; pick sequencing determines the retrieval
sequence of line items. Batching, one of the most frequently
used strategies for the pick process, is designed to reduce the
average travel time per order by sharing a pick tour with other
orders. Batch picking is sometimes called group picking or consolidation
picking. Rhea (1985) reports a successful case study in the cosmetic
industry to significantly increase the system throughput by batching
and other strategies as well.
There are basically two criteria for batching: the
proximity of pick locations and the time window. Proximity batching
assigns each order to a batch based on proximity of its S/R locations
to those of other orders. The major issue in proximity batching
is how to measure the proximities among orders, which implicitly
assumes a pick sequencing rule to visit a set of locations. In
general, the pick sequencing rule depends on the equipment type,
which is the subject of the next section. The problem of obtaining
an optimal proximity batching strategy can be formulated as a
vehicle routing problem (VRP) but in a more complicated form;
see Golden and Assad (1986) for a review on the VRP. Unfortunately,
the relationship does not provide any new insights to our problem,
since the VRP is already one of the most difficult problems in
combinatorial optimization.
Chisman (1975) and (1977) presents two heuristics
for the batching problem by considering the underlying VRP. Elsayed
(1981), and Elsayed and Stern (1983) develop several heuristics
for proximity batching. Their heuristics consist of two phases:
first, select a 'seed' order; second, add an order at a time
based on the proximity of pick locations. Platzman and Bartholdi
(1985) develop a general framework for proximity batching based
on the spacefilling curve, which is a simple, flexible heuristic
for the traveling salesman problem; see Bartholdi and Platzman
(1988b) for other applications of the heuristic. Hwang and Lee
(1988a) give a batching algorithm for person-aboard S/RS. Using
a measure of pairwise proximity, they consider several heuristics
which are categorized as agglomerative or sequential. For the
examples considered, their heuristics outperform those of Elsayed
and Stern, and Hwang, Baek, and Lee (1988).
Elsayed (1988), and Elsayed and Unal (1989) consider
proximity batching rules with and without due time constraints.
Their simulation results for person-aboard S/RS favor a heuristic
similar to those of Elsayed and Stern. Mutel and Anciaux (1989)
present analytical models for batching and storage rules in a
warehouse with an aisle configuration.
Using simulation, Gibson (1990) examines the effects
of the following factors on travel time:
He reports that a suitable batching rule used in
conjunction with CLASS yields significant reductions in average
batch tour lengths; in some instances these reductions are 44%.
Under time window batching, the orders arriving during
the same time interval (fixed or variable length), called a time
window, are grouped as a batch. These orders are then processed
simultaneously in the following stages (Quinn 1983). Time window
batching requires minimal analysis effort, and still seems to
achieve a significant reduction in travel time, which is a major
portion of total process time. Few results with general applicability
are available for time window batching (Choe 1991).
Zoning is closely related to batching, although it
may be implemented with or without batching; see Sharp, Choe,
and Yoon (1990) for various combinations of batching and zoning.
Zoning divides the entire picking area into several zones with
each picker dedicated to select the line items only in his or
her zone. In some cases zones naturally correspond to each equipment
type in the pick area if an OPS has several different types of
S/R equipment. In other cases zones are artificially determined.
The major advantages of zoning are familiarity of the picker
with his or her zone and travel time reduction, because of the
smaller area coverage by each picker.
Depending on the process sequence, zoning may be
further classified into two types: progressive zoning and synchronized
zoning. Under progressive zoning, each batch (possibly of one
order) is processed only by one zone at a time; at any particular
point in time each zone processes a batch that is different from
the others. Hence, the batch is finished only after it sequentially
visits all the zones containing its line items. Under synchronized
zoning, all the zones are working on the same batch at the same
time. There may be some idle times of zone pickers to wait until
all the zone pickers finish the current batch. This synchronization
of pickers is intended to keep the batches from being mixed, and
so to lessen the complexity of the following stages such as the
A/SS.
The major difference between the two types is whether
a batch is split into suborders (in synchronized zoning) or not
(in progressive zoning). Synchronized zoning usually gives a
shorter response time at the expense of order integrity than does
progressive zoning. However, synchronized zoning requires an
additional system, the A/SS, to recover order integrity, while
progressive zoning usually does not require such a system. It
is not straightforward to compare directly one zoning type with
the other. Moreover, an OPS may use both types of zoning; 'small'
orders in terms of the number of zones visited are processed by
progressive zoning, while large ones are processed by synchronized
zoning.
Despite the significant impact of zoning on the performance
of OPS, zoning has received little attention in the literature.
Armstrong, Cook, and Saipe (1979) consider an OPS with proximity
batching and synchronized zoning. For the FLA-OPS with both the
PS and the A/SS, they formulate a mixed-integer program to minimize
the total process time, and then solve the problem by Bender's
decomposition method. For a rack system with item picking, Mellema
and Smith (1988) evaluate the effects of various factors on system
performance: storage rule, aisle configuration, and batching
and zoning rules. Their simulation model shows that operation
with both batching and zoning significantly increases picker utilization.
However, the comparison is not conclusive, because their model
does not include the A/SS, which is a direct consequence of the
decision to use batching and zoning.
Choe (1991) seems to be the only analytical results
with general applicability which can evaluate the efficiency of
both time window batching and synchronized zoning. The results
provide a quick analytical tool for a MSS-OPS with conventional
racks and A/SS. The rack system is of ladder layout (no intermediate
cross aisles), and pickers selects items under selective one-way
traffic (pickers are not allowed to turn around in the middle
of an aisle). Using a prototype example, the results indicate
that time window batching can significantly increase the system
capacity, and synchronized zoning with time window batching can
increase it further.
Aside from batching and zoning, there are many alternatives
to improve the efficiency of OPS. For example, a 'good' design
that provides suitable (physical and/or mental) aiding systems
for humans might yield an OPS more efficient than a highly automated
OPS; in some cases automation is used as a quick solution rather
than the best one (Weber 1989). After considering human factors
in automated warehousing systems, Yates (1989) points out that
modern technology for automation in warehousing will eliminate
some human factors but at the expense of introducing others.
Therefore, a real OPS should be designed as an integrated system
of hardware, software, and 'humanware'. Of course, this issue
is not peculiar to order picking, but a fundamental question arising
in most engineering applications.
For order picking Gross (1981) estimates that, depending
on the type of warehouse, 30% to 40% of the labor cost can be
associated with the pick operation. The author then suggests
rules-of-thumb to reduce the labor cost. Falk (1983) deals with
an illumination system in automated and manual warehouses. Mital
(1983), Mital and Asfour (1983), and Bienkowski et al. (1986)
attempt to develop a data base for determining time standards
of various material handling activities such as lifting, lowering,
pushing, pulling, and carrying. Armbruster (1988) presents various
issues in human factors of manual OPS and suggests some designs
of work environments. Lewis and Lin (1989) focus on manual lifting
in the electronics industry.
Considering a real warehouse, Riaz-Kahn (1984) develops
a model which gives the time standards of a human picker in a
conventional warehouse with racks and aisles. The time standards
consist of three components: load time, travel time, and miscellaneous
time. The estimation of travel time, however, is based on a naive
aisle routing rule that generates the pick tour from prenumbered
storage locations.
One may use a computer aided system for order picking
to simplify the tasks of human pickers (Frazelle 1988). For example,
the computer aided system may provide several features as follows:
In addition to reduced labor cost, Gross (1981) and
Gupta (1982) claim high accuracy resulting from such computer
aided systems as their major advantage. They also report that,
in some cases, the computer aided OPS with human pickers are more
efficient in terms of both throughput and cost than highly automated
OPS. Rhea (1985) reports a successful case study where the 'friendly'
work environments for human pickers, along with the participation
of employees during the design process, can dramatically improve
system performance. Shirk and Bredenbeck (1987) give an example
of an automated documentation system that consists of radio-linked,
mobile computer terminals. Tolliver (1989) observes that, for
a manual OPS, a light-directed pick system with automated data
entry reduces human errors by 95%, and increases productivity
by 10%.
The primary objective of the A/SS is to re-establish
order integrity that is lost during the pick process. The A/SS
takes various forms including, at opposite ends of the spectrum,
manual staging and high-volume automated sortation system. A
number of articles are mainly concerned with the general treatment
of the A/SS: Walsh (1979) for the components of high-volume A/SS;
Emerson and Schmatz (1981) and Gupta (1982) for a kitting matrix
(a manual-staging type of A/SS); Suzuki (1981) for issues in A/SS;
Cox (1983) for a case study of the A/SS design; Horrey (1983)
for various alternatives of A/SS.
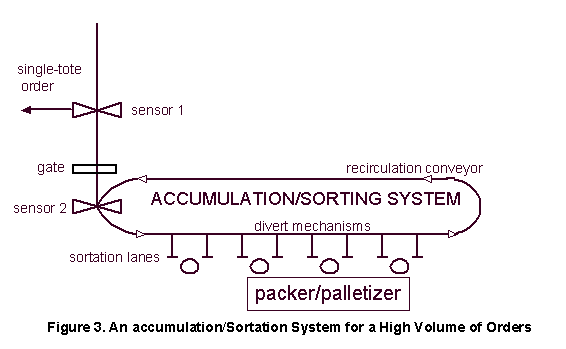
The high-volume automated A/SS as shown in Figure
3 usually has a closed-loop conveyor, automated divert mechanisms,
and accumulation lanes. This type of A/SS is of our interest,
since it requires large initial and operating costs as well as
space. The high-volume A/SS usually processes a wave (or batch
of orders) in the following way:
1. each wave is released into the A/SS according to the wave release rule.
2. as the sensor identifies the order corresponding to an incoming (or recirculated) item, usually in a container (e.g. a tote), it assigns the item to one of the available lanes, if possible.
3. otherwise, the item yet assigned is recirculated.
A few results with general applicability have appeared
in the literature. Bozer and Sharp (1985) elaborate the issues
in the operation of an A/SS in which each order is pre-assigned
to an accumulation lane, e.g. according to the shipping door corresponding
to the order. Their A/SS can be found in FLA- and MLA-OPS. Using
simulation, they evaluate the throughput of the system as a function
of the induction capacity, the number of lanes, the length of
lanes, the presence of a recirculation loop, and the control system.
(Reprinted
from Yoon and Sharp 1990)
Bozer, Quiroz, and Sharp (1988) then study a different
type of A/SS which processes a batch in which the number of orders
is greater than the number of lanes. A typical example of this
A/SS is the sorting area A of the MSS-OPS shown in Figure 1.
In this case the throughput of the system is determined mainly
by the number of recirculations. Their simulation, which focuses
on the lane assignment strategy and the wave release strategy,
shows that incidental assignment achieves the greatest throughput
among the assignment rules considered. Under incidental assignment,
the sensor assigns any incoming item (belonging to an order yet
assigned) into one of the available lanes, regardless of any other
considerations.
Few analytical results are reported in the literature.
Murphy and Stohr (1978) develop analytical models for a sortation
process such as the check processing system of a bank, which however
is not applicable to our A/SS. Santana and Platzman (1979) formulate
a Markov decision process for the A/SS with many accumulation
lanes and one packer, which is not applicable to most real A/SS
either. Regarding recirculation as the major bottleneck of A/S
operation, Choe (1991) develop a quick, rough method to determine
the mean and variance of A/S times. It is indeed a formidable
task to develop an analytical model which is able to describe
the movement of recirculated items on the loop conveyor and the
releasing pattern of items into the A/SS.
The analysis of A/SS itself is of interest also because
it is related to a number of problems arising in other areas,
such as the kitting operation in electronics assembly (Sellers
and Nof 1986), and postal sortation (Vrgoc and Ceric 1988). Bozer,
Quiroz, and Sharp point out the similarity to the operation of
an AGV system with a single, closed-loop path (Bartholdi and Platzman
1989), and information retrieval from computer drum storage (Fuller
1977). In addition, the features of the A/SS are similar to the
retrial queue (Yang and Templeton 1987), and the random coverage
problem (Yadin and Zacks 1982).
Palletizing or packing is a common material handling
activity in the OPS. Obviously, it is the major activity in the
shipping area. A less obvious palletizing problem occurs in the
multiple stocking problem and the inventory packing problem as
mentioned earlier. Our discussion here is confined to the practical
palletizing problem (PPP): find an optimal loading rule to palletize
a set of (3-dimensional) items into a set of (3-dimensional) containers
such as pallets or boxes. The objective function of the PPP is
either to maximize the volume utilization of a pallet or to minimize
the total number of pallets used for a given set of items. The
resulting pallet should be capable of enduring some physical forces
and constraints during its handling and transportation.
In fact, the PPP is a complicated 3-dimensional version
of a classical optimization problem, the bin packing problem (BPP).
The BPP can be defined as either a 1-dimensional problem (1-BPP)
by 1-dimensional items and containers, or a 2-dimensional problem
(2-BPP) in a similar manner. The 1-BPP can be applied to the
storage problem of computer files in computer memory; the 2-BPP
to a cutting-stock problem which maximizes the number of 'small'
items taken away from 'large' material sheets. The BPP has received
considerable attention in the literature; see Coffman, Garey,
and Johnson (1984), and Tsai, Malstrom, and Meeks (1988) for literature
reviews.
Since even the 1-BPP is (NP-) hard, most research
attempts have been directed to obtaining a fast, good heuristic
for the PPP. Hodgson (1982) classifies the PPP into two categories:
the manufacturer's PPP (M-PPP) and the distributor's PPP (D-PPP).
In the M-PPP the manufacturer palletizes identical products to
identical pallets which are shipped in turn by standardized trucks.
The M-PPP is usually used for a long-term plan to maximize the
volume utilization of a pallet, and so to minimize the handling
and transportation costs. On the other hand, the D-PPP packs
various items of a customer order into possibly more than one
pallet. Consequently, the D-PPP varies with each customer order,
and must be solved quickly to be applicable for daily and hourly
operation.
Few results for the PPP have appeared in the literature.
It is remarkable that palletizing itself is one of the most common
activities performed in warehouses and distribution centers, but
analytical results are very limited, probably due to the apparent
complexity of the problem. See Schreiner (1986), Szielasko (1988),
and Roach and Hunt (1988) for case studies of palletizing systems
in industry. In general, heuristics for the PPP are based on
two concepts; layer building and column building. Layer building
is a bottom-to-top method to build a pallet by stacking a 'horizontal'
layer of items on the top of others. The pattern in a layer then
can be solved by the 2-BPP; e.g. Smith and de Cani (1980), and
Dowsland (1987). Column building is a side-to-side method to
construct and place the columns or stacks side by side.
George and Robinson (1980) is an early article which
explicitly deals with the D-PPP. Instead of developing an optimization
model, they present a heuristic model containing rules-of-thumb.
Their rules employ layer building along with other considerations
in real palletizing operation. For the 2-BPP, Hodgson (1982)
develop a heuristic based on a dynamic program. By refining the
heuristic (Hodgson, Hughes, and Martin-Vega 1983), Carlo et al.
(1985) implement a generalized heuristic for the D-PPP in a personal
computer.
Using an interactive simulation model, Kulick (1982)
attempts to find a loading pattern of the M-PPP. He suggests
using an interlocking pattern (turning 180 degrees from the layer
below using the same pattern) so that the resulting pallet can
resist the physical forces and stresses during handling and transportation.
For a similar problem, Carpenter and Dowsland (1985) develop
a layer-building method with a heuristic by Bischoff and Dowsland
(1982) for finding a pattern in each layer. They find that palletizing
by a 'single-minded' layer heuristic may not be suitable for practical
use. They suggest some additional stability criteria for practical
considerations in handling and transportation.
Puls and Tanchoco (1986), Penington and Tanchoco
(1988) are concerned with a prototype robotic palletizer for the
M-PPP. The unique feature of their heuristic is that it incorporates
the physical limitation of robots. For example, they devise a
loading sequence of a pallet so that the gripper of the robot
cannot interfere with the boxes already on the pallet.
Han, Knott, and Egbelu (1989) develop an L-pattern
heuristic for the M-PPP, a hybrid of layer and column building,
which places the base layer on the pallet, and then stacks boxes
by column building. In order to determine the detailed pattern
within a layer they use a dynamic program similar to that of Steudel
(1979) for the 2-BPP. Their heuristic yields better performance
than does a conventional method (by the General Services Administration
1966) in terms of volume utilization.
Issues in the design and operation of each equipment
type include the following aspects:
Some of the issues such as storage rule, batching,
and zoning, have been explained in the previous section. This
section is concerned with issues peculiar to each equipment type,
including racks, storage drawers, AS/RS, carousels, etc.
Racks and storage drawers are the oldest and still
the most popular equipment type for order picking. There are
various types of racks such as pallet racks, gravity flow racks,
bin shelving, etc. The major advantages of a rack system include
low initial and maintenance costs; its major disadvantages include
the difficulties in storing high-security items. Storage drawers,
usually limited to storage of small parts, may yield high space
utilization and security as well. However, both equipment types
become inefficient for retrieval in a large pick area. Despite
the popularity of these equipment types, few studies have appeared
in the literature.
Bassan, Roll, and Rosenblatt (1980), and Rosenblatt
and Roll (1984), along with some earlier works, are concerned
with the aisle layout of a conventional warehouse. Their results
are limited for pallet retrieval under SC operation. Rosenblatt
and Roll develop a procedure by considering simultaneously the
layout, storage policies, and space requirements. Malmborg and
Deutch (1988) present a model to evaluate aisle layout under DC
operation.
Few results are available for the aisle layout under
MC operation. This is partly due to the complexity of travel
time estimation involving the notorious traveling salesman problem
inherent to aisle routing. Mayer (1961) is one of the earlier
works for the estimation of travel time in a conventional warehouse
with racks and aisles. The aisle configuration is of the ladder
type, in which the layout consists of multiple parallel aisles
without intermediate cross aisles. He deals with only SC and
DC travel time. Kunder and Gudehus (1975) develop approximations
for MC travel time in the same layout under three simple aisle
routing heuristics. In their model the travel time estimation
is a function of the number of pick locations which are assumed
to be uniformly distributed.
For the pick sequencing problem under MC operation,
Ratliff and Rosenthal (1983) give an efficient algorithm to find
a shortest path to visit a set of pick locations in a ladder layout.
No probabilistic analysis of this problem is reported in the
literature. Goetschalckx and Ratliff (1988a) extend the previous
problem to one with wide aisles. A wide aisle is roughly defined
as an aisle of more than 3.7 m (or 12 ft.) width. For a system
with wide aisles, one must find the travel sequence from one aisle
to another and also find the pick sequence within a wide aisle.
For a ride-and-pick system with the same configuration, Goetschalckx
and Ratliff (1988b) consider a clustering method to give a set
of pick locations to be visited at each vehicle stop, since the
travel time from one side to the other within the same aisle is
no longer negligible.
Finding an optimal path in a general layout is a
formidable task, since the underlying traveling salesman problem
is notoriously difficult to solve exactly in a reasonable computing
time. For a general layout, Bartholdi and Platzman (1988a) develop
a simple heuristic based on the spacefilling curve. Their heuristic
requires minimal effort for implementation and is flexible enough
for dynamic environments where the pick sequencing problems may
change even as they are being solved. Its performance, however,
depends on the efficiency of the underlying spacefilling curve,
which should be custom-designed for each application.
One of the important issues related to aisle routing
is that the picker should stack the items as he or she picks them.
Especially for a pick-to-pack system (a system in which the picker
has to make the selected items ready for shipping as he or she
returns to the I/O point at the end of each tour), an optimal
path should be based not only on the shortest travel time, but
also on the minimum packing time (usually by minimizing the number
of re-packing operations). Donaldson (1989) reports an expert
system, called WHEEL, with both routing and packing considerations
which also provides information for control and management. The
OPS for which the system is installed has a general layout with
'dead-end' aisles and SKUs with limited stackability.
Another issue in the OPS with an aisle configuration
is traffic congestion. Easily overlooked in the literature, the
aisle configuration in conjunction with the types of vehicles
commonly used might result in severe congestion. For example,
Ottjes and Hoogenes (1988) develop a simulation model to estimate
system throughput for a heavy traffic system.
Recently, automation technology has been applied
to the S/R operation in OPS, which has been one of the major tasks
of humans. Although this type of automation is limited so far
to pallet retrieval, the AGVs with S/R devices for handling pallets
can successfully substitute for human pickers. Menon, Kapoor,
and Blackman (1988) present a design model for an AGV system applied
to a pallet-retrieval warehouse with racks and aisles.
For gravity flow racks, Houmas (1986) gives a regression
model for cost analysis. The resulting cost equation has four
terms depending on the depth and length of the shelf frame, the
number of lanes, and the number of shelves. Nepola (1985) presents
a case study for a large-scale gravity flow rack system in the
dairy industry. O'Brien (1986) reports a real example of a single-aisle
gravity flow rack system, which is used for high-activity items.
For the design of the system the author examines various strategies
such as layout, replenishment cycle, and storage rule.
Storage drawers have received less attention. Herrera-Cuellar
and Sharp (1983) develop an algorithm that minimizes the cost
of the drawers and cabinets used. Their procedure employs a regression
model for cost analysis, a rectangle packing heuristic, and a
two-step heuristic for the 2-BPP, and produces the detailed storage
location assignment of each SKU as well as the total number of
drawers and cabinets.
In general, automated storage and retrieval systems
can be classified into three types: unit-load AS/RS, miniload
AS/RS, and person-aboard S/RS. This classification is not exhaustive.
For example, the storage rack of the AS/RS may be more than one
lane deep (Shieh 1985, Szielasko 1988); the S/R machine can carry
more than one pallet at the same time (Rizo-Patron, Bozer, and
McGinnis 1983, Jaikumar and Solomon 1986); the S/R machine can
visit more than one lane (Hwang and Ko 1988, Schmidt 1989, Baumbach
et al. 1989, Park and Webster 1989b).
The major advantages of this automated equipment
(except the person-aboard S/RS) include the precision, accuracy,
and speed in S/R activity. The AS/RS becomes an attractive alternative
when the space available is limited; the AS/RS requires minimal
floor space because items can be stored much higher than in conventional
equipment types. The disadvantages of the AS/RS, like other sophisticated
systems, include high initial and maintenance costs, and significant
engineering and design efforts.
The unit-load AS/RS has received the greatest attention
in the literature among various types of AS/RS. Since the operation
of a unit-load AS/RS is typically limited to SC and DC operation,
the problems associated with its design and operation seem less
complicated.
Design of unit-load AS/RS: Practical guidelines
for the design and installation of unit-load AS/RS can be found
in White (1980), Zollinger (1982), Bafna (1983), and Bafna and
Solt (1983). In addition, Zollinger gives a general cost model;
Bafna and Solt present a 'rough' estimator of the size of the
pallet rack. Bailey (1985) focuses on the cost comparison of
AS/RS with manual S/R systems. According to the cost comparison,
the AS/RS might not be justified unless its operational and managerial
advantages are considered.
The approaches for the design of unit-load AS/RS
can be analytical models or computer aided systems. In most analytical
approaches the S/R machine travel time is the basic quantity for
evaluating system performance, such as the maximum throughput
of the system, the response time of an order, and the utilization
rate of the S/R machine. Hausman, Schwarz, and Graves (1976)
obtain an expected SC travel time for the square-in-time rack
with CLASS; Graves, Hausman, and Schwarz (1977) obtain an expected
DC travel time for the square-in-time rack; Bozer and White (1984)
give the expected SC and DC travel times for racks of general
shape with RANDS; Choe and Sharp (1989) develop estimators for
the SC and DC travel times in general racks with CLASS. Rosenblatt
and Eynan (1989) explore the structure of SC travel time in the
square-in-time rack (given by Hausman, Schwarz, and Graves) to
find a fast algorithm for an optimal partitioning rule. Their
model deals with SC travel time only.
Karasawa, Nakayama, and Dohi (1980) give an analytical
model for the design of the unit-load AS/RS. Using a non-linear
mixed integer programming formulation, their model determines
the number of S/R machines, the desired speed of a S/R machine,
and the size of a rack, under the throughput and space constraints.
However, their scope is limited, since only SC operation with
RANDS is permitted.
For a similar problem, Ashayeri, Gelders, and Wassenhove
(1985) develop an analytical model to determine the number of
aisles and the configuration of an aisle. The objective function
is the total life-time cost including the costs of S/R machines,
racks, building, buffer space, land, maintenance, and order picking
labor. For the throughput estimation they use a rough approximation
of DC travel time in RANDS.
Illingworth and Sharp (1988) present an optimization
model to overcome some of the drawbacks of previous models, such
as the limited consideration of the effects of operating decisions
on system throughput. For example, their model can evaluate the
effects of DC operation in CLASS. They solve the resulting nonlinear
program by a search procedure.
Azadivar (1986) focuses on the buffer space in front
of the AS/RS rather than the AS/RS itself. The author formulates
a stochastic program to find the maximum throughput with constraints
such as the buffer size of incoming pallets and the response time
of retrieval orders. Some of the parameters in the problem are
estimated by simulation. Those results can be applied to the
design of the buffer space.
High equipment costs of the unit-load AS/RS may not
be justified for a system with low S/R activity requirements.
In this case Hwang and Ko (1988) suggest a multi-aisle unit-load
AS/RS where the number of S/R machines are fewer than the number
of aisles. They develop travel time estimators, a procedure for
specifying the parameters of CLASS, and the number of S/R machines
to meet the throughput requirement.
For an overcrowded unit-load AS/RS, Hackman and Rosenblatt
(1990) formulate a storage allocation problem which determines
what quantities of which items should be assigned to the AS/RS.
The unassigned items are stored in a secondary storage area.
Their heuristic yields less cost for handling the overflows than
does the COI rule applied to that problem.
Due to the limited scope of an analytical approach,
a number of attempts have been made to develop a computer aided
system for the design of unit-load AS/RS. The major advantage
of this approach, mainly with simulation modules, is its ability
to represent all the details of the system, such as the interface
of the AS/RS and other subsystems (e.g. in- and out-bound conveyors),
and the performance evaluation of the AS/RS in dynamic environments.
Aside from general-purpose simulation languages, the following
computer aided systems are developed for AS/RS and other material
handling systems: e.g. Ulgen and Elayat (1981), Ashayeri, Gelders,
and Looy (1983), Bailey (1983), Carson et al. (1983), Perry, Hoover,
and Freeman (1983) and (1984), Raghunath, Perry, and Cullinane
(1986), Ashayeri and Gelders (1989).
Control of unit-load AS/RS: Obviously, DC operation
of the S/R machine seems more efficient than SC operation. The
gains from DC operation, however, depend on the efficiency of
order sequencing to determine the pair of storage and retrieval
locations on the same DC trip. For the unit-load AS/RS, re-sequencing
of storage orders (or incoming pallets) is usually difficult,
while re-sequencing of retrieval order is much easier (retrieval
orders are nothing more than messages). Therefore, the order
sequencing problem attempts to find a retrieval order well matched
with a given storage location. Note that in SC operation, sequencing
of retrieval orders is identical to sequencing jobs on a single
machine, which is a well-known problem in scheduling theory (Kusiak,
Hawaleshka, and Cormier 1985).
Han et al. (1987) examine two heuristics for the
order sequencing problem: the nearest-neighbor heuristic and
the shortest-leg heuristic. In their examples the nearest-neighbor
heuristic increases the throughput by about 15%. Seidmann (1988)
is also concerned with the same retrieval sequencing problem but
in dynamic environments. Using an artificial intelligence approach,
the so-called state-operator framework, he presents a dynamic
adaptive control scheme to determine the pair of storage and retrieval
locations in real-time operation. Dagli and Wasti (1989) develop
a dynamic control scheme for the order sequencing problem in a
unit-load AS/RS for perishable items.
The interface with other subsystems are crucial to
the performance of the whole system. For a conveyor-fed AS/RS,
Sharp, Kittel, and Hollender (1989) evaluate the effect of various
factors on system performance. The factors considered include
storage rule, conveyor configuration, buffer size, S/R machine
velocities, and workload imbalance among subsystems. Everton
(1989) and Takakuwa (1989) deal with the interface problem which
determines the best configuration among various alternatives of
conveyor- and/or AGV- fed AS/RS.
Workload equalization seems an effective control
strategy for the system in dynamic environments, especially with
high fluctuation in order volume; that fluctuation is quite common
in real systems. Jaikumar and Solomon (1985) solve the workload
equalization problem to utilize the S/R machines during the light-workload
period by relocating some pallets closer to the I/O for the heavy-workload
period.
One may try to evaluate the effectiveness of those
issues by considering them simultaneously rather than by separating
one from others. This approach makes it possible to show the
interactions among various strategies, but only by simulation.
Considering a real warehouse, Waugh and Ankener (1977) evaluate
the effects of various factors on the performance of unit-load
AS/RS. According to their results, the issues shown below are
crucial to system efficiency:
Schwarz, Graves, and Hausman (1978) report similar
results, that CLASS with DC operation can significantly increases
the system throughput, and also that the stochastic behavior of
a unit-load AS/RS is similar to that of a single-server queue.
Linn and Wysk (1987), similar to the previous approach,
examine the dynamic performance of unit-load AS/RS with seasonal
fluctuations in order volume. They focus on the dwell rule, the
retrieval order sequencing, the method of forecasting order volume,
and storage rule. Their simulation result imply that
Linn and Wysk (1990) then develop an expert system
to control the AS/RS. First, they classify the domain knowledge
into two types: strategic knowledge and tactical knowledge.
The issues above fall into strategic knowledge; other issues such
as rules for overflows and/or machine failures into tactical knowledge.
They develop a rule-based expert system based on results available
in the literature.
The major difference between the miniload and unit-load
AS/RS is the size of units to be handled. In the miniload AS/RS
the unit of each SKU is usually so small that each storage location
can contain more than one unit. A typical retrieval quantity
of a line item is less than the number of units stored in a storage
location, and so the container extracted for picking is usually
re-stored after the retrieval of the appropriate quantity. In
this case the miniload AS/RS may have more than one pick position
at the I/O point so that the S/R machine does not have to wait
until the picker finishes the current S/R activity. Some miniload
AS/RS may be equipped with 'remote' order pickers and/or workstations
connected by a conveyor delivery system. Other variations of
miniload AS/RS can be found as in the case of unit-load AS/RS.
Zollinger (1982) seems to be the only study for cost
analysis of miniload AS/RS. The container and rack costs are
separated from the S/R machine cost, and total costs depend on
container size, weight of SKUs, height of the rack, height of
the S/R machine, and the controller.
Because of the similarity to unit-load AS/RS, most
results for unit-load AS/RS can be applied to miniload AS/RS,
although this may not yield any new insights for miniload AS/RS.
For example, the estimators of SC and DC travel times in the
unit-load AS/RS with RANDS are still valid in the miniload AS/RS
with the same storage rule; however, the total time of a DC cycle
in the miniload AS/RS with two pick locations should include the
'possible' idle time of the S/R machine due to the imbalance of
pick and travel times. Bengtson and Gomez (1988), and Pulat and
Pulat (1988) develop simulation models for miniload AS/RS. Bozer
and White (1988), and Sharp et al. (1988) present models for the
design of miniload AS/RS. Both models are capable of evaluating
the interactions between the picker and the S/R machine.
Using simulation, Medeiros, Enscore, and Smith (1986)
consider the storage rule in a single-aisle miniload AS/RS with
two pick positions. In their example they observe that CLASS
with 2 classes increases the system throughput by about 10%, and
that CLASS with more than three classes has a negligible additional
effect on throughput.
For a single-aisle miniload AS/RS with two pick positions,
Foley and Frazelle (1990) develop analytical expressions for the
distribution of DC travel time and system throughput in a square-in-time
rack with RANDS. Their formulae give the maximum throughput in
closed form when the pick time is deterministic or exponential.
The miniload AS/RS is widely used for central storage
of work-in-process (WIP) inventory in a manufacturing system.
Cobbin (1986) shows a simulation model for such miniload AS/RS,
which is sometimes referred to as the tote stacker. Using a miniload
AS/RS with a single S/R machine and 8 workstations, Kaylan and
Medeiros (1988) show that CLASS works significantly better for
high WIP level, and that the zone configuration in CLASS is crucial
to such efficiency gains. These applications to manufacturing
are not of our major interest.
The unique feature of the person-aboard S/RS, a semi-automated
system, is that the picker aboard the S/R machine is able to perform
many S/R jobs between successive visits to the I/O point. Subsequently,
the pick sequencing problem to find a shortest path to visit a
set of S/R locations is crucial to the efficiency of the person-aboard
S/RS.
This pick sequencing problem turns out to be a variation
of the traveling salesman problem (TSP) with the Chevychev norm,
since the machine travel time follows the Chevychev norm; see
Lawler et al. (1985) for a comprehensive treatment of the TSP.
The following results for the pick sequencing problem have appeared
in the literature: Bozer (1985), Elsayed and Unal (1989) for
expected travel time; Bozer, Schorn, and Sharp (1985), Bachers,
Dangelmaier, and Warnecke (1988), Goetschalckx and Ratliff (1988c),
Guenove and Raeside (1989) for comparison of various heuristics.
Summarizing, several heuristics for the construction and improvement
of a pick sequence are good enough for practical use; the length
of resulting paths from those heuristics is quite often close
(within 5%) to the optimal length.
Oudheusden, Tzen, and Ko (1988) examine various strategies
for person-aboard S/RS such as pick sequencing and storage rule.
As mentioned earlier, they apply the CORAS to find a pair of
SKUs which is stored in opposite locations across the aisle.
They then consider assigning the pairs within an aisle under DEDIS.
Extracting the set of representative orders and tours from historical
data, they formulate the SLAP as a set partitioning problem.
In order to solve the problem, they use a two-phase heuristic;
first, obtain an exact optimal solution of that problem but with
a smaller representative set; second, use a 2-opt (or pairwise-interchange)
procedure to solve the larger problem. Applying their procedure
to a real person-aboard S/RS, they report significant savings
in travel time.
The carousel is a relatively old technology in material
handling, and yet it has applications to various areas such as
order picking (Lombardi 1985, Kobuki 1987), WIP storage in a manufacturing
system (Bagadia 1982, Fredrick 1982), and kitting operations (Engwall
1985). The carousel brings the line items before the picker by
rotating the shelves with containers (e.g. totes). Depending
the direction of rotation, carousels are categorized as horizontal
carousels, vertical carousels, or rotary racks. The horizontal
and vertical carousels rotate carriers, consisting of shelves,
to position the appropriate container at the I/O point in horizontal
(clockwise or counter-clockwise) and vertical (upward or downward)
direction, respectively. The rotary rack consists of several
tracks (group of shelves as a rotation unit) which are able to
rotate in different directions from each other (Tielker 1989).
In general, carousels offer good space utilization
and high throughput (Weiss 1980). The vertical carousel usually
exposes only one level of shelves at a time and provides excellent
item protection and security but at higher costs; see Bredenbeck,
Shirk and Majure (1989) for an example. While the rotary rack
is the least common and most expensive type, its major advantage
is a significant reduction in picker idle time and the feasibility
of multiple I/O points.
Most studies in the literature focus on the horizontal
carousel, since it is the most common type; fortunately, most
results for the horizontal carousel (except cost analysis) are
directly applicable to the vertical carousel. The unique circular
structure of the carousel requires a different treatment from
those for another equipment types.
Mardix and Sharp (1985) analyze the cost structure
of horizontal carousels. Their analysis shows that the equipment
cost mainly depends on the weight capacity, number of containers,
and the number of levels (or height of the carousel). They then
proceed to a performance analysis focusing on the workload balancing
problem to maximize picker utilization. Assuming a uniform and
independent distribution of S/R locations, their simulation and
analytical results imply that
Generalizing their models, Bulla (1987) and Sharp
et al. (1990) develop a design procedure that considers various
operating factors.
Based on the previous cost analysis, Hwang and Lee
(1988b) present a constrained optimization model for the determination
of system size to minimize the life-time cost of a single carousel
system. They develop an approximation of rotation time with an
assumption that the S/R locations are uniformly and independently
distributed over the carousel. Their approximation method is
similar to one in Han and McGinnis (1986). In addition to travel
time estimation, Han and McGinnis consider an order sequencing
problem similar to one of Han et al. (1987) for the unit-load
AS/RS.
The results presented so far assume that an order
requests only one line item. Thus, those results are not compatible
with order picking, where most orders request more than one line
item. In this situation the pick sequencing problem becomes important
to efficient operation of the carousel system. Bartholdi and
Platzman (1986) examine a pick sequencing problem in a single
carousel system. They present an optimal algorithm, along with
several heuristics of which the performance becomes quite close
to the optimal one with heavy workload. A similar problem is
considered by Stern (1986). In addition to pick sequencing, he
presents a Markovian model (similar to one by Mardix and Sharp)
to evaluate system performance, and a heuristic for storage location
assignment based on SOTAST.
The pick sequencing problem with both horizontal
rotation time of the shelves and vertical moving time of the (robot)
picker is treated by Wen and Chang (1988). Wen, Lin, and Chang
(1989) then extend the problem to a double carousel system. Modifying
the heuristics in Wen and Chang, they show that simple heuristics
can yield a significant increase in throughput.
The SLAP for the carousel system has a unique feature
that the relative distance of a storage location to the I/O point
varies as the carousel rotates. In other words, there is no location
'close' to the I/O point which can be easily identified in other
equipment types. Consequently, the performance of a storage rule
in the carousel system is directly related to the pick sequencing
rule used.
Let us consider a simpler problem, that is, the SLAP
in a single carousel system with a single level of shelves. Here
we do not need to consider the vertical travel time of the picker,
and there is no interference associated with that time component.
Then, the following storage rule, the so-called 'organ pipe arrangement'
for a single-level carousel with FCFS order retrieval, minimizes
the expected total rotation time of an order regardless if its
size, the number of line items, is fixed or random (Lim, Bartholdi,
and Platzman 1985):
1. sort the SKUs in decreasing order of S/R activity frequency.
2. store the most 'popular' SKU anywhere on the carousel.
3. assign subsequent SKUs to alternating positions
to the left and the right of the first SKU.
The organ pipe arrangement derives its name from
the fact that the resulting bar chart depicting the S/R frequency
of each SKU resembles organ pipes. In fact, this storage rule
is developed for a specific type of computer information storage
systems, called a linear storage system (Hardy, Littlewood, and
Polya 1952, Bergmans 1972).
A 2-dimensional extension of the problem for a typical
multi-level carousel, unfortunately, is not straightforward.
The 2-dimensional problem is (NP-) hard (Bergmans 1972), and does
not even have an asymptotically optimal heuristic storage rule
based solely on the ranking of S/R activity (Karp, McKeller, and
Wong 1975). A review of the results for computer information
storage can be found in Wong (1980). Lim, Bartholdi, and Platzman
explore several extensions of the organ pipe arrangement to the
multi-level carousel. In general, questions on the optimal storage
rule for carousels mostly remain unanswered.
The system where a picker operates more than one
carousel is of particular interest because of the apparent gains
in productivity. The analysis of such multi-carousel systems,
however, becomes more complicated by the interaction among carousels
and the picker. For example, one carousel becomes idle if the
picker is still working on the other at the time that the carousel
positions a container at the I/O point. Moreover, the picker
usually require some transition time to move from one carousel
to the other. These situations are often referred to as 'machine
interference'. It is a common phenomenon where an operator is
in charge of more than one machine.
The machine interference problem has received considerable
attention in the literature; see Stecke and Aronson (1985) for
a review. For example, Koenisberg (1986), and Kim and Koenisberg
(1987) present applications of the machine interference problem
to a carousel system. The operation of a multi-carousel system
is still a research area with significant potential.
The carousel system is also frequently used for a
central storage of WIP inventory. In this case the carousel system
is usually linked to workstations by conveyors. Such a system
is studied by Koenisberg and Mamer (1982). They develop an approximate
queueing model for the performance evaluation of the entire manufacturing
system. In their model the machine interference problem is applied
to the performance evaluation of the carousel system as a subsystem.
Buley and Knott (1986) elaborate the basic design
issues for a rotary rack. As the results for the multi-carousel
system suggest, the rotary rack with as many tracks as the number
of levels might cost too much, yet yield little rewards in system
performance. Buley and Knott solve a simpler version of the problem
which determines the number of tracks to meet a constraint on
picker idle time.
For a rotary rack with as many tracks as the number
of levels, Han, McGinnis, and White (1988) develop travel time
estimators and study the order sequencing problem by extending
the work of Han and McGinnis (1986).
The discussion so far has focused on the S/R equipment
types. Although other equipment types are just as important to
OPS as the S/R equipment type, those are beyond the scope of this
research. We mention here some results relevant to order picking.
Handling equipment is as crucial to OPS as arteries
are to the body. In our point of view, the major issues in handling
equipment are associated with the layout of the OPS and the interface
with each S/R equipment. General issues in handling equipment
include the selection of equipment type, the determination of
vehicle fleet size, and control rules such as dispatching rule:
see Muth and White (1979) for an overview on conveyors, Mueller
(1983) for an overview on AGV systems, Bode (1988) for an overview
on industrial trucks, and Kulwiec (1985) for overviews and practical
guidelines on various equipment types.
Auxiliary equipment types, such as identification
systems, controllers/sensors, and data transfer systems, provide
information transfer crucial to the efficient management of OPS,
although they do not physically handle items: see Naval Supply
Systems Command (1985) for an overview and specifications of auxiliary
equipment type, and Rylander (1987) and Lacagnina (1989) for identification
and control systems.
The major objective of this report is the presentation
of a general analysis framework for the design and operation of
an OPS with an emphasis on item picking. Elaborating a systematic
design procedure of the OPS, one may view the subject as a multifaceted
system of great dimensional complexity, and identify various issues
and their interwoven structure.
Analytical approaches for the design of OPS seemingly
fail to give satisfactory answers to a complicated real case.
Moreover, it is not likely in the foreseeable future that one
can develop a universal, analytical model which leads to an efficient
design of real OPS. On the other hand, the use of non-analytical
approaches is also limited. For example, the simulation approach
is clearly not able to address all the possible alternatives during
the design process. The expert system approach is questionable
because of the lack of sufficient domain knowledge (Permann and
Bailey 1988). Consequently, an approach with great potential
is to develop a computer aided system which combines analytical
models, simulation models, human expert knowledge, and the planner's
insights (Yoon and Sharp 1990). The major task of this approach
would be the specification of which knowledge source is more suitable
for which decision in the design process.
The performance evaluation of operating strategies
is a fertile area for investigation. Questions related to storage
assignment, batching and zoning strategies, order and pick sequencing
rules, etc., need to be addressed. Sortation and palletizing
strategies have received little attention, despite their importance.
Also, an efficient information management system corresponding
to the resulting operating scheme is crucial to their implementation
and further improvement in practice.
Another important issue in the operation of OPS is
the evaluation of operating strategies in dynamic environments,
and also the development of dynamic operating schemes. For example,
instead of one-time storage assignment, one may develop a dynamic
control scheme for stock reallocation, dynamic stocking, and workload
equalization. Stock reallocation is frequently required in modern
warehouses because of the shorter life cycle and diversification
of products. Dynamic stocking for an item pick system is the
method of stocking only those SKUs that will be selected during
the next shift. Workload equalization will be crucial to OPS
with high fluctuation in order volume.
The performance characteristics of individual equipment
types such as AS/RS and carousel have been addressed in many studies.
However, some newer, higher throughput devices, such as rotary
racks, automatic item picker, and multi-shuttle miniload AS/RS,
have not been fully examined. Moreover, it is certain that the
number of new equipment types will keep growing. In addition,
some older equipment types such as a rack system with multi-command
operation certainly need more attention.
Another equipment-related area that offers potential
is the design of work stations for pickers and for packers. Work
station improvements in conjunction with computer aided order
picking can improve productivity by a factor of two and more.
Packing often requires as much labor as picking, which points
to a potential area of research. Even for a sophisticated and
automated OPS, the human factors and human-machine interface should
be carefully designed in order to achieve successful systems.
Amagai, K. 1985. TAKENAKA Plan/Design Service Procedure
for Physical Distribution Facilities. Proc. of the 6th International
Conference on Automation in Warehousing, 77-84.
Armbruster, R. 1988. Ergonomics in Warehousing.
Proc. of the 9th International Conference on Automation in Warehousing,
283-293.
Armstrong, R. D., W. D. Cook and A. L. Saipe. 1979.
Optimal Batching in a Semi-Automated Order Picking System. J.
Opl. Res. Soc. 30, 711-720.
Ashayeri, J., and L. F. Gelders. 1985. Warehouse
Design Optimization. Euro J. O. R. 21, 285-294.
Ashayeri, J., and L. F. Gelders. 1989. Simulation
Program Generator for AS/RS Systems. Proc. of the 10th International
Conference on Automation in Warehousing, 211-219.
Ashayeri, J., L. F. Gelders and P. M. van Looy. 1983.
A Simulation Package for Automated Warehouses. Matl. Flow 1,
189-198.
Ashayeri, J., L. Gelders and L. van Wassenhove. 1985.
A Microcomputer-Based Optimisation Model for the Design of Automated
Warehouses. Int. J. Prod. Res. 23, 825-839.
Azadivar, F. 1986. Maximization of the Throughput
of a Computerized Automated Warehousing System Under System Constraints.
Int. J. Prod. Res. 24, 551-556.
Azadivar, F. 1987. Minimum-Cost Modular Design of
Automated Warehousing Systems. Matl. Flow 4, 177-188.
Azadivar, F. 1989. Optimum Allocation of Resources
between the Random Access and Rack Storage Spaces in an Automated
Warehousing Systems. Int. J. Prod. Res. 27, 119-131.
Bachers, R., W. Dangelmaier and H. J. Warnecke. 1988.
Selection and Use of Order-Picking Strategies in a High-Bay Warehouse.
Matl. Flow 4, 233-245.
Bafna, K. M. 1983. Procedures for Investigating AS/RS
Feasibility and Suitability Are Outlined for IEs. Ind. Eng. 15,
June, 60-66.
Bafna, K. M., and F. R. Solt. 1983. Procedures Given
for Determining AS/RS System Size and Preparing Specs. Ind. Eng.
15, August, 76-81.
Bagadia, K. S. 1982. Carousel System and Distribution
Concept Applied to Tool Cribs. Proc. of the 1982 Annual IIE Conference,
211-213.
Bailey, M. 1983. Computer-Aided Design for Automated
Warehouses. Proc. of the 5th International Conference on Automation
in Warehousing, 113-126.
Bailey, M. 1985. Economic Modelling of AS/RS. Proc.
of the 6th International Conference on Automation in Warehousing,
45-55.
Bartholdi, III., J. J., and L. K. Platzman. 1986.
Retrieval Strategies for a Carousel Conveyor. IIE Trans. 19,
166-173.
Bartholdi, III., J. J., and L. K. Platzman. 1988a.
Design of Efficient Bin-Numbering Schemes for Warehouses, Matl.
Flow 4, 247-254.
Bartholdi, III, J. J., and L. K. Platzman. 1988b.
Heuristics Based on Spacefilling Curves for Combinatorial Problems
in Euclidean Space. Mgmt. Sci. 34, 291-305.
Bartholdi, III, J. J., and L. K. Platzman. 1989.
Decentralized Control of Automated Guided Vehicles on a Single
Loop. IIE Trans. 21, 76-81.
Bassan, Y., Y. Roll and M. J. Rosenblatt. 1980. Internal
Layout Design of a Warehouse. AIIE Trans. 12, 317-322.
Baumbach, J., V. Englert, J. C. Ammons and R. Schmidt.
1989. Design and Analysis of the Satellite Storage and Retrieval
System (SS/RS). Presented at the Material Handling Focus '89,
Material Handling Research Center, Georgia Institute of Technology,
Atlanta, Georgia.
Bengtson, N. M., and R. J. Gomez. 1988. Why a Single
Aisle Miniload System Is Not Simple to Model. Proc. of the 1988
Winter Simulation Conference, 603-608.
Bergmans, P. P. 1972. Minimizing Expected Travel
Time on Geometrical Patterns by Optimal Probability Rearrangements.
Info. & Cont. 20, 331-350.
Bienkowski, T. L., S. S. Asfour, S. W. Waly and A.
M. Genaidy. 1986. A Comprehensive Data Base for the Design of
Manual Material Handling. Proc. of the 8th Annual Conference
on Computers and Industrial Engineering, 351-354.
Bischoff, E., and W. B. Dowsland. 1982. An Application
of the Micro to Product Design and Distribution. J. Opl. Res.
Soc. 33, 271-280.
Bode, W. 1988. Industrial Trucks within Centralized
Material Flow Systems. Matl. Flow 4, 225-232.
Bozer, Y. A. 1985. Optimizing Throughput Performance
in Designing Order Picking Systems. Ph.D. Dissertation. School
of Industrial and Systems Engineering, Georgia Institute of Technology,
Atlanta, Georgia.
Bozer, Y. A., M. A. Quiroz and G. P. Sharp. 1987.
Simulation for Automated Accumulation and Sortation Systems. Unpublished
Report, Material Handling Research Center, Georgia Institute of
Technology, Atlanta, Georgia.
Bozer, Y. A., M. A. Quiroz and G. P. Sharp. 1988.
An Evaluation of Alternative Control Strategies and Design Issues
for Automated Accumulation and Sortation Systems. Matl. Flow
4, 265-282.
Bozer, Y. A., E. C. Schorn and G. P. Sharp. 1985.
An Evaluation of Heuristics for In-the-Aisle Order Picking. Report
TR-85-15, Material Handling Research Center, Georgia Institute
of Technology, Atlanta, Georgia.
Bozer, Y. A., and G. P. Sharp. 1985. An Empirical
Evaluation of a General Purpose Automated Order Accumulation and
Sortation System Used in Batch Picking. Matl. Flow 2, 111-131.
Bozer, Y. A., and J. A. White. 1984. Travel Time
Models for Automated Storage/Retrieval Systems. IIE Trans. 16,
329-338.
Bozer, Y. A., and J. A. White. 1988. Design and Performance
Models for End-Of-Aisle Order Picking Systems. Report TR-87-08,
Material Handling Research Center, Georgia Institute of Technology,
Atlanta, Georgia.
Branigan, M. J. 1988. Visual Interactive Simulation
for Automated Warehouse Design. Proc. of the 9th International
Conference on Automation in Warehousing, 157-167.
Bredenbeck, J. E., W. T. Shirk and J. C. Majure.
1989. Small Parts Handling Needs Are Met by Installing a Vertical
Storage System. Ind. Eng. 21, July, 34-38.
Buley, D. T., and K. Knott. 1986. Designing Vertical
Carousels to Maximize Operator Utiliztion. Proc. of the 8th Annual
Conference on Computers and Inustrial Engineering, 271-275.
Bulla, T. L. C. 1987. Efficient Carousel Configurations
for Work-In-Process Storage. Report TD-86-12, Material Handling
Research Center, Georgia Institute of Technology, Atlanta, Georgia.
Camp, R. E. 1990. Storage Requirements Are Determined
Through the Use of Simulation. Ind. Eng. 22, March, 44-48.
Carew, V. 1989. The Navy's Warehouse Utilization
Program. Presented at the Material Handling Focus '89, Material
Handling Research Center, Georgia Institute of Technology, Atlanta,
Georgia.
Carlo, H., T. J. Hodgson, L. A. Martin-Vega and E.
R. Stern. 1985. MICRO-IPLS: Pallet Loading on a Microcomputer.
Comp. Ind. Eng. 9, 29-34.
Carpenter, H., and W. B. Dowsland. 1985. Practical
Considerations of the Pallet-Loading Problem. J. Opl. Res. Soc.
36, 489-497.
Carson, Jr., J. S., C. H. Wysowski, W. A. Johnson
and N. Wilson. 1983. A GPSS Model of a Unit Load AS/R System and
Shipping Department. Proc. of the 1983 Winter Simulation Conference,
193-196.
Chisman, J. A. 1975. The Clustered Traveling Salesman
Problem. Comp. Opns. Res. 2, 115-119.
Chisman, J. A. 1977. Optimizing the Shipping Function.
J. Ind. Eng. 9, 38-41.
Choe, K. 1991. Aisle-Based Order Pick Systems with
Batching, Zoning, and Sorting. Unpublished Ph.D. Dissertation,
School of Industrial and Systems Engineering, Georgia Institute
of Technology, Atlanta, Georgia.
Choe, K., and G. P. Sharp. 1988. Class-Based Storage
with Multi-Command Operation. Report TR-88-08, Material Handling
Research Center, Georgia Institute of Technology, Atlanta, Georgia.
Choe, K., and G. P. Sharp. 1989. Class-Based Storage
in a Unit-Load AS/RS. Report TR-89-08, Material Handling Research
Center, Georgia Institute of Technology, Atlanta, Georgia.
Cobbin, P. 1986. Modeling Tote Stacker Operation
as a WIP Storage Device. Proc. of the 1986 Winter Simulation
Conference, 597-605.
Coffman, E. G., Jr., M. R. Garey and D. S. Johnson.
1984. Approximation Algorithms for Bin-Packing - An Updated Survey.
Algorithm Design for Computer System Design, G. Ausiello, M.
Lucertini and P. Serafini (Eds.), Springer-Verlag, New York, 49-106.
Cox, B. 1983. Using Standard Data and CAD Techniques
to Design an Automated Parcel Sorting Facility. Proc. of the
5th International Conference on Automation in Warehousing, 149-157.
Cox, B. 1986. Determining Economic Levels of Automation
by Using a Hierarchy of Productivity Ratios Techniques. Proc.
of the 7th International Conference on Automation in Warehousing,
39-49.
Dagli, C. H., and S. N. Wasti. 1989. Intelligent
Operations Planning in Automatic Storage and Retrieval. Proc.
of the 1989 IIE Integrated Systems Conference and Society for
Integrated Manufacturing Conference, 511-516.
Davies, A. L., M. C. Gabbard and E. F. Reinholdt.
1983. Storage Method Saves Space and Labor in Open-Package-Area
Picking Operations. Ind. Eng., 15, June, 68-74.
Dichtl, E., and W. Beeskow. 1980. Optimal Allocation
of Commodities in Warehouses by Means of Multi-Dimensional Scaling
(in German). Zeitschrift Optns. Res. 24, B51-B64.
Donaldson, T. 1989. KODAK's Expert System for Order
Picking. Presented at the Material Handling Focus '89, Material
Handling Research Center, Georgia Institute of Technology, Atlanta,
Georgia.
Dowsland, K. A. 1987. A Combined Data-Base and Algorithmic
Approach to the Pallet-Loading Problem. J. Opl. Res. Soc. 38,
341-345.
Elliott, K. A. 1986. Designing Warehousing Systems.
Presented at the 36th Annual Material Handling Short Course, Material
Handling Research Center, Georgia Institute of Technology, Atlanta,
Georgia.
Elsayed, E. A. 1981. Algorithms for Optimal Material
Handling in Automatic Warehousing Systems. Int. J. Prod. Res.
19, 525-535.
Elsayed, E. A. 1988. Order Batching Algorithms for
AS/R Interlaving Systems with/without Due Time Constraints. Presented
at the Material Handling Focus '88, Material Handling Research
Center, Georgia Institute of Technology, Atlanta, Georgia.
Elsayed, E. A., and R. G. Stern. 1983. Computerized
Algorithms for Order Processing in Automated Warehousing Systems.
Int. J. Prod. Res. 21, 579-586.
Elsayed, E. A., and O. I. Unal. 1989. Order Batching
Algorithms and Travel-Time Estimation for Automated Storage/Retrieval
Systems. Int. J. Prod. Res. 27, 1097-1114.
Emamizadeh, B., and K. Knott. 1986. Matching Unit
Load and Inventory Systems. Proc. of the 8th Annual Conference
on Computers and Industrial Engineering, 105-108.
Emerson, C. R., and D. S. Schmatz. 1981. Results
of Modeling an Automated Warehouse System. Ind. Eng. 13, August,
28-33.
Engwall, R. L. 1985. Automated Material Handling
in Electronic Assembly. Prsented at the Annual Material Handling
Users Conference, Material Handling Research Center, Georgia Institute
of Technology, Atlanta, Georgia.
Evans, J. R. 1984. The Factored Transportation Problem.
Mgmt. Sci. 30, 1021-1024.
Everton, J. G. 1989. Improving Automated Storage/Retrieval
System Performance Through the Use of Advanced Simulation Systems.
Proc. of the 10th International Conference on Automation in Warehousing,
37-41.
Falk, N. 1983. Warehouse Lighting - It Costs or Pays:
An Energy Management Approach. Proc. of the 5th International
Conference on Automation in Warehousing, 219-224.
Fisher, E. L., J. B. Farber and M. G. Kay. 1988.
MATHES: An Expert System for Material Handling Equipment Selection.
Eng. Cost. Prod. Econo. 14, 297-310.
Foley, R. D., and E. H. Frazelle. 1990. Analytical
Results for Miniload Throughput and the Distribution of Dual Command
Travel Time. to appear in IIE Trans.
Francis, R. L., L. F. McGinnis and J. A. White. 1983.
Locational Analysis. Euro. J. O. R. 12, 220-252.
Francis, R. L., and J. A. White. 1974. Facility
Layout and Location: An Analytical Approach. Prentice Hall, Englewood
Cliffs, New Jersey.
Frazelle, E. H. 1988. Small Parts Order Picking:
Equipment and Strategy. Report OP-88-01, Material Handling Research
Center, Georgia Institute of Technology, Atlanta, Georgia.
Frazelle, E. A., and G. P. Sharp. 1989. Correlated
Assignment Strategy Can Improve Any Order-Picking Operation.
Ind. Eng. 21, April, 33-37.
Frazelle, E. H., and G. P. Sharp. 1988. How to Design,
Operate, Select, and Improve Order Picking Systems. Presented
at the Order Picking Workshop, Material Handling Research Center,
Georgia Institute of Technology, Atlanta, Georgia.
Fredrick, C. 1982. Our Automatic Carousels Slash
Manufacturing Time. Mod. Matl. Handl. June.
Fuller, S. H. 1972. An Optimal Drum Scheduling Algorithm.
IEEE Trans. Comp. C21, 1153-1165.
Gelders, L., and J. Ashayeri. 1989. Lessons Learned
from Automation: Theory versus Practice. Proc. of the 10th International
Conference on Automation in Warehousing, 15-20.
General Services Administration. 1966. Warehouse
Operations. U.S. Government Printing Office, Washington, D.C.
George, J. A., and D. F. Robinson. 1980. A Heuristic
for Packing Boxes into a Container. Comp. Opns. Res. 7, 147-156.
Gibson, D. R. 1990. Order Batching Procedures. Report
TD-90-05, Material Handling Research Center, Georgia Institute
of Technology, Atlanta, Georgia.
Goetschalckx, M. 1983. Storage and Retrieval Policies
for Efficient Order Picking Operations. Ph.D. Dissertation, School
of Industrial and Systems Engineering, Georgia Institute of Technology,
Atlanta, Georgia.
Goetschalckx, M., and J. Ashayeri. 1988. Classification
and Design of Order Picking Systems. Report TR-88-14, Material
Handling Research Center, Georgia Institute of Technology, Atlanta,
Georgia.
Goetschalckx, M., and H. D. Ratliff. 1987. Optimal
Lane Depth for Single and Multiple Products in Block Stacking
Storage Systems. Report TR-87-01, Material Handling Research Center,
Georgia Institute of Technology, Atlanta, Georgia.
Goetschalckx, M., and H. D. Ratliff. 1988a. Order
Picking in an Aisle. IIE Trans. 20, 53-62.
Goetschalckx, M., and H. D. Ratliff. 1988b. An Efficient
Algorithm to Cluster Order Picking Items in a Wide Aisle. Eng.
Cost. Prod. Econo. 13, 263-271.
Goetschalckx, M., and H. D. Ratliff. 1988c. Sequencing
Picking Operations in a Man-Aboard Order Picking System. Matl.
Flow 4, 255-263.
Golden, B. L., and A. A. Assad. 1986. Perspectives
on Vehicle Routing: Exciting New Developments. Opns. Res. 34,
803-810.
Grasso, E. T., and J. M. A. Tanchoco. 1983. Unit
Load and Material Handling Considerations in Material Requirements
Planning Systems. Matl. Flow 1, 79-87.
Graves, S. C., W. H. Hausman and L. B. Schwarz. 1977.
Storage-Retrieval Interleaving in Automatic Warehousing Systems.
Mgmt. Sci. 23, 935-945.
Gross, J. G. 1981. Picking Methods May Provide Key
to Lower Cost Warehouse Plans. Ind. Eng. 13, June, 50-54.
Gudehus, T. 1973. Principles of Order Picking: Operations
in Distribution and Warehousing Systems (in German), W. Girardet,
Essen, West Germany.
Guenove, M., and R. Raeside. 1989. Real Time Optimization
of Man on Board Order Picking. Proc. of the 10th International
Conference on Automation in Warehousing, 89-93.
Gupta, N. K. 1982. Kitting Matrix Adds Accuracy to
Small Part Picking System. Ind. Eng. 14, January, 35-38.
Hackman, S. T., and M. J. Rosenblatt. 1990. Allocating
Items to an Automated Storage and Retrieval System. IIE Trans.
22, 7-14.
Hall, N. G. 1989. The Inventory Packing Problem.
Nav. Res. Log. 36, 399-418.
Han, C. P., K. Knott and P. J. Egbelu. 1989. A Heuristic
Approach to the Three-Dimensional Cargo-Loading Problem. Int.
J. Prod. Res. 27, 757-774.
Han, M. -H., and L. F. McGinnis. 1986. Automated
Work-in-Process Carousels: Modeling and Analysis. Report TR-86-06,
Material Handling Research Center, Georgia Institute of Technology,
Atlanta, Georgia.
Han, M. -H., L. F. McGinnis, J. S. Shieh and J. A.
White. 1987. On Sequencing Retrievals in an Automated Storage/Retrieval
System. IIE Trans, 19, 56-66.
Han, M. -H., L. F. McGinnis and J. A. White. 1988.
Analysis of Rotary Rack Operation. Matl. Flow 4, 283-293.
Hanelt, H., and K. D. Kryder. 1989. Designs-Phasing
of Computer Integrated Automated Distribution Centers to Benefit
Corporate Growth. Proc. of the 10th International Conference
on Automation in Warehousing, 53-62.
Hardy, G. H., J. E. Littlewood and G. Polya. 1952.
Inequalities, Cambridge University, Cambridge, UK.
Harmatuck, D. J. 1976. A Comparison of Two Approaches
to Stock Location. Logis. Transp. Rev. 12, 282-285.
Hatanaka, S. 1989. Recent Technical Trends of Automated
Storage Systems in Japan. Proc. of the 10th International Conference
on Automation in Warehousing, 23-28.
Hausman, W. H., L. B. Schwarz and S. C. Graves. 1976.
Optimal Storage Assignment in Automatic Warehousing Systems.
Mgmt. Sci. 22, 629-638.
Herrera-Cuellar, A., and G. P. Sharp. 1983. Modular
Drawer Storage Systems: A Design Procedure. Report TR-83-08, Material
Handling Research Center, Georgia Institute of Technology, Atlanta,
Georgia.
Heskett, J. L. 1963. Cube-Per-Order Index - A Key
to Warehouse Stock Location. Transp. Distn. Mgmt. 3, 27-31.
Hodgson, T. J. 1982. A Combined Approach to the Pallet
Loading Problem. IIE Trans. 14, 175-182.
Hodgson, T. J., D. S. Hughes and L. A. Martin-Vega.
1983. A Note on a Combined Approach to the Pallet Loading Problem.
IIE Trans. 15, 268-271.
Hodgson, T. J., and T. J. Lowe. 1982. Production
Lot Sizing with Material-Handling Cost Considerations. IIE Trans.
14, 44-51.
Horrey, R. J. 1983. Sortation Systems: From Push
to High-Speed Fully Automated Applications. Proc. of the 5th
International Conference on Automation in Warehousing, 77-83.
Houmas, C. G. 1986. Comparing Small Parts Storage
Systems. Report TD-86-04, Material Handling Research Center, Georgia
Institute of Technology, Atlanta, Georgia.
Hwang, H., W. Baek and M.-K. Lee. 1988. Clustering
Algorithms for Order Picking in an Automated Storage and Retrieval
System. Int. J. Prod. Res. 26, 189-201.
Hwang, H., and C. S. Ko. 1988. A Study on Multi-Aisle
System Served by a Single Storage/Retrieval Machine, Int. J.
Prod. Res. 26, 1727-1737.
Hwang, H., and M.-K. Lee. 1988a. Order Batching Algorithms
for a Man-on-Board Automated Storage and Retrieval System. Eng.
Cost. Prod. Econo. 13, 285-294.
Hwang, H., and M. -K. Lee. 1988b. An Approach in
the Design of a Unit-Load Automated Carousel System. Eng. Opt.
13, 197-210.
Illingworth, L., and G. P. Sharp. 1988. Comparative
Analysis of Unit-Load Storage Systems Using a PC-Based Program.
Report TR-86-18, Material Handling Research Center, Georgia Institute
of Technology, Atlanta, Georgia.
Jaikumar, R., and M. M. Solomon. 1985. Dynamic Operational
Policies in an Automated Warehouse. Report 85-44, Northeastern
University.
Jaikumar, R., and M. M. Solomon. 1986. Real-Time
Control of Multiple Command Cycle Storage-Retrieval Warehousing
Systems. Proc. of the 7th International Conference on Automation
in Warehousing, 155-158.
Juenemann, R., and F. Meister. 1988. Rational Warehouse
Planning - EDP-Supported. Matl. Flow 4, 217-223.
Kallina, C., and J. Lynn. 1976. Appilication of the
Cube-Per-Order Index Rule for Stock Location in a Distribution
Warehouse. Interfaces 7, 37-46.
Karasawa, Y., H. Nakayama and S. Dohi. 1980. Trade-off
Analysis for Optimal Design of Automated Warehouses. Int. J.
Sys. Sci. 11, 567-576.
Karp, P. M., A. C. McKeller and C. K. Wong. 1975.
Near Optimal Solutions to a Two-Dimensional Placement Problem.
SIAM J. Comp. 4, 271-286.
Kay, E. 1968. A Mathematical Model for Handling
in a Warehouse. Pergamon Press, Oxford.
Kaylan, A., and D. J. Medeiros. 1988. Analysis of
Storage Policies for Miniload AS/RS. Eng. Cost. Prod. Econo.
13, 311-318.
Kearney, A. T. 1984. Measuring and Improving Productivity
in Physical Distribution. National Council of Physical Distribution
Management, Oak Brooks, Illinois.
Kim, J., and A. Seidman. 1990. Storage Assignment
Policies in Automatic/Retrieval Systems. Working Paper, School
of Business Administration, University of Rochester.
Kim, W. B., and E. Koenisberg. 1987. The efficiency
of Two Groups of N Machines Served by a Single Robot. J. Opl.
Res. Soc. 38, 523-538.
Kibuki, M. 1987. Piece Picking Using a Carousel System.
Proc. of the 8th International Conference on Automation in Warehousing,
283-293.
Koenisberg, E. 1986. Analysis of the Efficiency of
Carousel and Tote-Stacker Performance. Proc. of the 7th International
Conference on Automation in Warehousing, 363-373.
Koenisberg, E., and J. Mamer. 1982. The Analysis
of Production Systems. Int. J. Prod. Res. 20, 1-16.
Kooy, E. D. 1984. Comparison of Order Picking Methods.
Working Paper, Pillsbury Co.
Kooy, E. D. 1985. Proposed Method of Determining
the Best Order Picking System. Working Paper, Pillsbury Co.
Krajacic, P. 1988. The Intelligent Picking Machine
for Sensitive Products. Proc. of the 9th International Conference
on Automation in Warehousing, 91-98.
Kulick, A. 1982. Interlocking Pallet Pattern Simulation
Program. Ind. Eng. 14, September, 22-24.
Kulkarni, V. G., and S. P. Sethi. 1989. Deterministic
Retrial Times are Optimal in Queues with Forbidden States. INFOR.
27, 374-386.
Kulwiec, R. A. (Ed.) 1985. Materials Handling Handbook,
2nd Ed. John Wiley & Sons, New York.
Kunder, R., and Gudehus, T. 1975. Mean Time for Collecting
Items from a Rectangular System of Shelves (in German). Zeitschrift
Optns. Res. 19, B53-B72.
Kusiak, A. 1985. Material Handling in Flexible Manufacturing
Systems. Matl. Flow. 2, 79-95.
Kusiak, A., O. Hawaleshka and G. Cormier. 1985. Order
Picking Policies in Automated Storage Systems. Proc. of the 6th
International Conference on Automation in Warehousing, 239-248.
Lacagnina, M. 1989. Next Generation Identification
and Control Systems. Presented at the Material Handling Focus
'89, Material Handling Research Center, Georgia Institute of Technology,
Atlanta, Georgia.
Lawler, E. L., J. K. Lenstra, A. H. G. Rinnoy Kan
and D. B. Shmoys (Eds.) 1985. The Traveling Salesman Problem.
John Wiley & Sons, New York.
Lewis, D. A., and R. Lin. 1989. Materials Handling
in the Electronics Industry: The Same Old Problems. Eng. Cost.
Prod. Econo. 16, 111-116.
Lim, S. 1990. Zoning in Storage Systems. Ph.D. Dissertation,
School of Industrial and Systems Engineering, Georgia Institute
of Technology, Atlanta, Georgia.
Lim, W. K., J. J. Bartholdi, III. and L. K. Platzman.
1985. Storage Schemes for Carousel Conveyors Under Real Time Control.
Report TR-85-10, Material Handling Research Center, Georgia Institute
of Technology, Atlanta, Georgia.
Linn, R. J., and R. A. Wysk. 1987. An Analysis of
Control Strategies for an Automated Storage/ Retrieval System.
INFOR. 25, 66-82.
Linn, R. J., and R. A. Wysk. 1990. An Expert System
Framework for Automated Storage and Retrieval System Control.
Comp. Ind. Eng. 18, 37-48.
Lombardi, R. 1985. Implementation of a Carousel Storage
and Retrieval System: Visual Graphics Case Study. Automated Material
Handling and Storage, Auerbach Publishers, Pennsauken, New Jersey.
Malmborg, C. J., and K. Bhaskaran. 1987. On the Optimality
of the Cube Per Order Index for Conventional Warehouse with Dual
Command Cycles. Matl. Flow 4, 169-175.
Malmborg, C. J., and K. Bhaskaran. 1989. Optimal
Storage Assignment for Multiaddress Warehousing Systems. IEEE
Trans. Sys. Man Cyber. 19, 197-205.
Malmborg, C. J., and K. Bhaskaran. 1990. A Revised
Proof of Optimality for the Cube-Per-Order Index for Stored Item
Location. Appl. Math. Model. 14, 87-95.
Malmborg, C. J., and S. J. Deutch. 1988. A Stock
Location Model for Dual Address Order Picking Systems. IIE Trans.
20, 44-52.
Malmborg, C. J., H. B. Hubbard and M. H. Agee. 1985.
Network Simulation Approaches to Material Handling Equipment.
Proc. of the 7th Annual Conference on Computers and Industrial
Engineering, 144-148.
Malmborg, C. J., B. Krishnakumar, G. R. Simons and
M. H. Agee. 1989. EXIT: A PC-Based Expert System for Industrial
Truck Selection. Int. J. Prod. Res. 27, 927-941.
Malmborg, C. J., G. R. Simmons and M. H. Agee. 1986.
Knowledge Engineering Approaches to Material Handling Specification.
Proc. of the 1986 Fall IE Conference, 148-151.
Mardix, I., and G. P. Sharp. 1985. Cost and Efficiency
Analysis of the Carousel Storage System. Report TR-85-08, Material
Handling Research Center, Georgia Institute of Technology, Atlanta,
Georgia.
Matson, J. O., S. R. Swaminathan and J. M. Mellichamp.
1990. Knowledge-Based Material Handling Equipment Selection.
Proc. of the 1990 International Industrial Engineering Conference,
212-217.
Matson, J. O., and J. A. White. 1982. Operational
Research and Material Handling. Euro. J. O. R. 11, 309-318.
Mayer, Jr., H. E. 1961. Storage and Retrieval of
Material. Western Elect. Engr. 5, 42-48.
Medeiros, D. J., E. E. Enscore, Jr. and A. D. Smith.
1986. Performance Analysis of Miniload Systems. Proc. of the
1986 Winter Simulation Conference, 606-612.
Mellema, P. M., and C. A. Smith. 1988. Simulation
Analysis of Narrow-Aisle Order Selection Systems. Proc. of the
1988 Winter Simulation Conference, 597-602.
Menon, S. R., S. G. Kapoor and R. B. Blackmon. 1988.
Navigation Planning for Mobile Robotic Devices in Modular Warehouses.
Int. J. Adv. Mfg. Tech. 3, 47-62.
Mital, A. 1983. Generalized Model Structure for Evaluating/Designing
Manual Material Handling Jobs. Int. J. Prod. Res. 21, 401-412.
Mital, A., and S. S. Ashfour. 1983. Material Handling
Capacity of Workers. Matl. Flow 1, 89-100.
Mullens, M. A. 1981. Use a Computer to Determine
the Size of a New Warehouse, Particularly in Storage and Retrieval
Areas. Ind. Eng. 13, June, 24-32.
Muller, D. J. 1989. AS/RS and Warehouse Modelling.
Proc. of the 1989 Winter Simulation Conference, 802-810.
Mueller, T. 1983. Automated Guided Vehicles. Springer-Verlag,
New York.
Murphy, F. H., and E. A. Stohr. 1978. A Mathematical
Programming Approach to the Scheduling of Sorting Operations.
Nav. Res. Log. Qt. 25, 155-167.
Mutel, B., and D. Anciaux. 1989. Study of Storage
and Picking Policies of Items in Large Delivery-Type Warehouse.
Proc. of the 10th International Conference on Automation in Warehousing,
Dallas, Texas.
Muth, E. J., and J. A. White. 1979. Conveyor Theory:
A Survey. AIIE Trans. 11, 270-277.
Naval Supply Systems Command. 1985. Warehouse Modernization
and Layout Planning Guide. NAVSUP Publication 529, Naval Publication
and Forms Center, Philadelphia, Pennsylvania.
Nepola, K. 1985. Automated Warehouse System for Carts
and Dollies. Proc. of the 6th International Conference on Automation
in Warehousing, 85-91.
O'Brien, J. W. 1986. Pharmaceutical Distribution
Improved Order Picking. Proc. of the 1986 Fall IE Conference,
476-480.
Ottjes, J. A., and E. Hoogenes. 1988. Order Picking
and Traffic Simulation in Distribution Centres. Int. J. Prod.
Dist. Mfg. Mgmt. 18, 14-21.
van Oudheusden, D. L., Y. -J. J. Tzen and H. -T.
Ko. 1988. Improving Storage and Order Picking in a Person-on-Board
AS/R System: A Case Study. Eng. Cost. Prod. Econo. 13, 273-283.
Page, E., and R. J. Paul. 1976. Multi-Product Inventory
Situations with One Restriction. Opns. Res. Qt. 27, 816-833.
Park, B. C. 1988. Closest Open Location Rule in AS/RS.
Working Paper, Department of Industrial Engineering, Keimyung
University, Taegu, Korea.
Park, B. C., and L. Platzman. 1987. Distribution
of the Closest Available Location in Automated Storage and Retrieval
Systems. Working Paper, School of Industrial and Systems Engineering,
Georgia Institute of Technology, Atlanta, Georgia.
Park, Y. H., and D. B. Webster. 1989a. Modelling
of Three-Dimensional Warehouse Systems. Int. J. Prod. Res. 27,
985-1003.
Park, Y. H., and D. B. Webster. 1989b. Design of
Class-Based Racks for Minimizing Travel Time in a Three-Dimensional
Storage System. Int. J. Prod. Res. 27, 1589-1601.
Penington, R. A., and J. M. A. Tanchoco. 1988. Robotic
Palletization of Multiple Box Sizes. Int. J. Prod. Res. 26, 95-105.
Perlmann, A. M., and M. Bailey. 1988. Warehouse Logistic
Systems - A CAD Model. Eng. Cost. Prod. Econo. 13, 229-237.
Perry, R. F., S. F. Hoover and D. R. Freeman. 1983.
Design of an Automated Storage/Retrieval System Using Simulation
Modeling. Proc. of the 5th International Conference on Automation
in Warehousing, 57-66.
Perry, R. F., S. V. Hoover and D. R. Freeman. 1984.
An Optimal-Seeking Approach to the Design of Automated Storage/Retrieval
Systems. Proc. of the 1984 Winter Simulation Conference. 349-354.
Platzman, L. K., and J. J. Bartholdi, III. 1985.
A Minimal Technology Method for Order Batching and Sequencing.
Report TR-85-04, Material Handling Research Center, Georgia Institute
of Technology, Atlanta, Georgia.
Pliskin, J. S., and D. Dori. 1982. Ranking Alternative
Warehouse Area Assignments: A Multiattribute Approach. IIE Trans.
14, 19-26.
Pulat, B. M., and P. S. Pulat. 1988. Performance
Analysis of Automatic Storage and Retrieval Systems - A Comparative
Approach. Proc. of the 1988 Winter Simulation Conference, 591-596.
Puls, F. M., and J. M. A. Tanchoco. 1986. Robotic
Implementation of Pallet Loading Patterns. Int. J. Prod. Res.
24, 635-646.
Quinn, E. B. 1983. Simulation of Order Processing
Waves. Presented at the Material Handling Focus '83, Material
Handling Research Center, Georgia Institute of Technology, Atlanta,
Georgia.
Raghunath, S., R. Perry and T. Cullinane. 1986. Interactive
Simulation Modeling of Automated Storage Retrieval Systems. Proc.
of the 1986 Winter Simualtion Conference, 613-620.
Ratliff, H. D., and A. S. Rosenthal. 1983. Order-Picking
in a Rectangular Warehouse: A Solvable Case of the Traveling Salesman
Problem. Opns. Res. 31, 507-521.
Rhea, N. W. 1985. New Clairol Product: Instant Productivity
in the Warehouse. Matl. Handl. Eng. July, 89-92.
Riaz-Kahn, M. 1984. An Efficiency Measurement Model
for a Computerized Warehousing System. Int. J. Prod. Res. 22,
443-452.
Rizo-Patron, A., Y. A. Bozer and L. F. McGinnis.
1983. Analytic and Simulation Models for Advanced Automated Storage/Retrieval
Systems. Report TR-82-04, Material Handling Research Center, Georgia
Institute of Technology, Atlanta, Georgia.
Roach, B., and K. Hunt. 1988. Finished Goods Sortation
and Palletizing in the Cigarette Industry. Proc. of the 9th International
Conference on Automation in Warehousing, 221-239.
Roll, Y., and M. J. Rosenblatt. 1983. Random versus
Grouped Storage Policies and Their Effect on Warehouse Capacity.
Matl. Flow 1, 199-205.
Roll, Y., M. J. Rosenblatt and D. Kadosh. 1989. Determining
the Size of a Warehouse Container. Int. J. Prod. Res. 27, 1693-1704.
Rosenblatt, M. J., and A. Eynan. 1989. Deriving the
Optimal Boundaries for Class-Based Automatic Storage/Retrieval
Systems. Mgmt. Sci. 35, 1519-1524.
Rosenblatt, M. J., and Y. Roll. 1984. Warehouse Design
with Storage Policy Considerations. Int. J. Prod. Res. 22, 809-821.
Rosenblatt, M. J., and Y. Roll. 1988. Warehouse Capacity
in a Stochastic Environment. Int. J. Prod. Res. 26, 1847-1851.
Rylander, R. 1987. Data Collection Within the Automated
Warehouse. Proc. of the 8th International Conference on Automation
in Warehousing, 323-329.
Santana, J. L., and L. K. Platzman. 1979. Real-Time
Scheduling of an "Open Warehouse" Sorter-Palletizer
System. Proc. of the 18th IEEE Conference on Decision and Control,
537-539.
Schall, S., and J. Chandra. 1989. Multiple Product
Inventory Policies with Unit Load and Storage Space Considerations.
Eng. Cost. Prod. Econo. 16, 245-256.
Schreiner, R. M. 1986. A Microcomputer-Based Pallet
Layout System to Evaluate and Improve Storage Space Utilization.
Proc. of the 8th Computers and Industrial Engineering, 87-90.
Schmidt, R. 1989. The Design of Satellite Storage
and Retrieval Systems with Random Access. Proc. of the 10th International
Conference on Automation in Warehousing, 159-164.
Schulze, L., and U. Westfal. 1989. Computer Aided
Warehouse Planning. Proc. of the 10th International Conference
on Automation in Warehousing, 45-49.
Schwarz, L. B., S. C. Graves and W. H. Hausman. 1978.
Scheduling Policies for Automatic Warehousing Systems: Simulation
Results. AIIE Trans. 10, 260-270.
Seidmann, A. 1988. Intelligent Control Schemes for
Automated Storage and Retrieval Systems. Int. J. Prod. Res. 26,
931-952.
Sellers, C. J., and S. Y. Nof. 1986. Part Kitting
in Robotic Facilities. Matl. Flow 3, 163-174.
Sharp, G. P. 1990. Intelligent Batching in Order
Picking. Presented at the 40th Annual Material Handling Short
Course, Material Handling Research Center, Georgia Institute of
Technology, Atlanta, Georgia.
Sharp, G. P., K. Choe and C. S. Yoon. 1990. Small
Parts Order Picking: Analysis Framework and Selected Results.
Report OP-90-04, Material Handling Research Center, Georgia Institute
of Technology, Atlanta, Georgia.
Sharp, G. P., J. Eckert, D. Gibson, C. G. Houmas
and I. Mardix. 1990. Order Picking Using Horizontal Carousels.
Report TR-89-01, Material Handling Research Center, Georgia Institute
of Technology, Atlanta, Georgia.
Sharp, G. P., E. H. Frazelle, R. D. Foley and D.
R. Gibson. 1988. Analysis and Configuration of Miniload AS/RS.
Working Paper, Material Handling Research Center, Georgia Institute
of Technology, Atlanata, Georgia.
Sharp, G. P., R. Kittel and K. J. Hollender. 1989.
Factors Affecting Productivity of a Pallet AS/RS. Proc. of the
10th International Conference on Automation in Warehousing, 105-111.
Shieh, J. S. 1985. On the Analysis of Selected Automated
Storage and Retrieval Systems. Ph.D. Dissertation, School of Industrial
and Systems Engineering, Georgia Institute of Technology, Atlanta,
Georgia.
Shirk, W. T. 1989. Material Flow Controls in a JIT
Environment. Presented at the Material Handling Focus '89, Material
Handling Research Center, Georgia Institute of Technology, Atlanta,
Georgia.
Shirk, W. T., and J. E. Bredenbeck. 1987. Portable
Terminals Boost Efficiency at AT&T. Matl. Hand. Eng. July.
Smith, D., and P. de Cani. 1980. An Algorithm to
Optimize the Layout of Boxes on Pallets. J. Opl. Res. Soc. 31,
573-578.
Stecke, K. E., and J. E. Aronson. 1985. Review of
Operator/Machine Interference Models. Int. J. Prod. Res. 23,
129-151.
Stern, H. I. 1986. Parts Location and Optimal Picking
Rules for a Carousel Conveyor Automatic Storage and Retrieval
System. Proc. of the 7th International Conference on Automation
in Warehousing, 377-385.
Steudel, H. J. 1979. Generating Pallet Loading Patterns:
A Special Case of the Two-Dimensional Cutting Stock Problem.
Mgmt. Sci. 25, 997-1004.
Steudel, H. J. 1983. Determination of Economic Pallet
Size for In-Plant Handling. Matl. Flow 1, 71-76.
Stone, H. S., and S. H. Fuller. 1973. On the Near
Optimality of the Shortest-Latency-Time-First Drum Scheduling
Discipline. Comm. ACM. 16, 352-353.
Suzuki, J. 1981. The Application and Suggestion of
Sorting Machine in Japan. Proc. of the 4th International Conference
on Automation in Warehousing, Tokyo, Japan.
Suzuki, S. 1988. Order Pattern Graph Assists Order
Picking System Design. Proc. of the 9th International Conference
on Automation in Warehousing, 113-124.
Szielasko, K. 1988. Future-Oriented Distribution
Centres with Automated Order Picking in High Performance Systems.
Proc. of the 9th International Conference on Automation in Warehousing,
67-84.
Takakuwa, S. 1989. Module Modeling and Economic Optimization
for Large-Scale AS/RS. Proc. of the 1989 Winter Simulation Conference,
795-801.
Tanchoco, J. M. A., and M. H. Agee. 1981. Plan Unit
Loads to Interact with All Components of Warehouse System. Ind.
Eng. 13, June, 36-48.
Tanchoco, J. M. A., R. P. Davis, P. J. Egbelu and
R. A. Wysk. 1983. Economic Unit Loads (EUL) for Multi-Product
Inventory Systems with Limited Storage Space. Matl. Flow 1, 141-148.
Tanchoco, J. M. A., R. P. Davis and R. A. Wysk. 1980.
Economic Order Quantities Based on Unit-Load and Material Handling
Considerations. Decis. Sci. 11, 514-521.
Tielker, U. G. 1989. Classification and Trends of
Order Picking Techniques. Proc. of the 10th International Conference
on Automation in Warehousing, 97-102.
Tolliver, R. 1989. Order Picking Basics at Avon Products.
Presented at the Material Handling Focus '89, Material Handling
Research Center, Georgia Institute of Technology, Atlanta, Georgia.
Tompkins, J. A., and J. A. White. 1984. Facilities
Planning. John Wiley & Sons, New York.
Tsai, R. D., E. M. Malstrom and H. D. Meeks. 1988.
A Two-Dimensional Palletizing Procedure for Warehouse Loading
Operations. IIE Trans. 20, 418-425.
Ulgen, O. M., and H. Elayat. 1981. GENSAWS: A General
Simulator for Automatic Warehousing Systems. Proc. of the 6th
International Conference on Automation in Warehousing, Novi Sad,
Yugoslavia.
Vemuganti, R. R. 1987. The Maximum Value of Inventory
and Shortages in Production Lot Size Systems. IIE Trans. 19,
404-411.
Vrgoc, M., and V. Ceric. 1988. Investigation and
Design of Parcel Sorting Systems in Postal Centres by Simulation.
Comp. in Ind. 10, 137-145.
Walsh, P. 1979. Carton Sortation in the Distribution
Warehouse. Proc. of the 3th International Conference on Automation
in Warehousing, 15-28.
Warehouse Education and Research Council. 1986.
Survey. Oak Brooks, Illinois.
Waugh, R. M., and R. A. Ankener. 1977. Simulation
of an Automated Stacker Storage System. Proc. of the 1977 Winter
Simulation Conference, 769-776.
Weber, H. 1989. The Humanistic Approach to Optimize
Logistic Concepts. Proc. of the 10th International Conference
on Automation in Warehousing, 319-325.
Weiss, D. J. 1980. Computer Controlled Carousels.
Proc. of the 3th International Conference on Automation in Warehousing,
Stratford, UK.
Wen, U. -P., and D. -T. Chang. 1988. Picking Rules
for a Carousel Conveyor in an Automated Warehouse. Omega 16,
145-151.
Wen, W. -P., J. T. Lin and D. -T Chang. 1989. Order
Picking for a Two-Carousel-Single-Server System in an Automated
Warehouse. Proc. of the 10th International Conference on Automation
in Warehousing, 65-70.
White, J. A. 1979. Picker to the Pick Face or Picking
Face to the Picker. Mod. Matl. Handling September, 19.
White, J. A. 1980. Auditing AS/R Systems after Installation.
Ind. Eng. 12, June, 20-21.
White, J. A. 1988. The Evolution of Materials Handling
in Warehousing. Proc. of the 9th International Conference on
Automation in Warehousing, 33-50.
White, J. A., and H. D. Kinney. 1982. Storage and
Warehousing. Handbook of Industrial Engineering. G. Salvendy
(ed.), John Wiley & Sons, New York.
Wilson, H. G. 1977. Order Quantity, Product Popularity,
and the Location of Stock in a Warehouse. AIIE Trans. 9, 230-237.
Wong, C. K. 1980. Minimizing Expected Head Movement
in One-Dimensional and Two-Dimensional Mass Storage System. Comp.
Surveys 12, 167-178.
Yadin, M., and S. Zacks. 1982. Random Coverage of
a Circle with Applications to a Shadowing Problem. J. Appl. Prob.
19, 562-577.
Yang, M. H. 1988. Analysis and Optimization of Class-Based
Dedicated Storage Systems. Report TD-88-07, Material Handling
Research Center, Georgia Institute of Technology, Atlanta, Georgia.
Yang, T., and J. G. C. Templeton. 1987. A Survey
on Retrial Queues. Queueing Systems 2, 201-233.
Yates, B. D. 1989. No Room for Automations in the
Automated Warehouse. Proc. of the 10th International Conference
on Automation in Warehousing, 149-154.
Yoon, C. S., and G. P. Sharp. 1990. Development of
an Intelligent Workstation for Order Pick System Analysis and
Design. Working Paper, Material Handling Research Center, Georgia
Institute of Technology, Atlanta, Georgia.
Zollinger, H. A. 1982. Planning, Evaluating and Estimating
Storage Systems. Presented at the 1st Annual Simulation Winter
Seminar, Institute of Matrial Management, Orlando, Florida.